题目内容
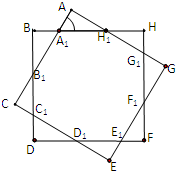 如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设∠AA1H1=α.
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设∠AA1H1=α.(1)试用α表示△AA1H1的面积;
(2)求八角形所覆盖面积的最大值,并指出此时α的大小.
考点:基本不等式在最值问题中的应用
专题:应用题
分析:(1)先求出AH1,再用α表示△AA1H1的面积;
(2)令t=sinα+cosα∈(1,
],只需考虑S△AA1H1取到最大值的情况.
(2)令t=sinα+cosα∈(1,
| 2 |
解答:
解:(1)设AH1为x,∴x+
+
=4,x=
,…(3分)
S△AA1H1=
•
=
,α∈(0,
),…(7分)
(2)令t=sinα+cosα∈(1,
],…(9分)
只需考虑S△AA1H1取到最大值的情况,
即为S=
=4-
,…(11分)
当t=
,即α=45°时,S△AA1H1达到最大 …(13分)
此时八角形所覆盖面积的最大值为64-32
. …(14分)
| x |
| sinα |
| x |
| tanα |
| 4sinα |
| sinα+cosα+1 |
S△AA1H1=
| 1 |
| 2 |
| x2 |
| tanα |
| 8sinαcosα |
| (sinα+cosα+1)2 |
| π |
| 2 |
(2)令t=sinα+cosα∈(1,
| 2 |
只需考虑S△AA1H1取到最大值的情况,
即为S=
| 4(t2-1) |
| (t+1)2 |
| 8 |
| t+1 |
当t=
| 2 |
此时八角形所覆盖面积的最大值为64-32
| 2 |
点评:本题考查利用数学知识解决实际问题,考查三角函数的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
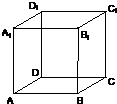 电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.
电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.