题目内容

5．设曲线y=ax2-lnx-a在点（1，0）处的切线方程为y=2（x-1），则a=（　　）
A．0B．$\frac{1}{2}$C．1D．$\frac{3}{2}$

分析 求出函数的导数，求得切线的斜率，由切线的方程可得a的方程，即可得到a．

解答 解：y=ax2-lnx-a的导数为y′=2ax-$\frac{1}{x}$，
可得在点（1，0）处的切线斜率为k=2a-1，
由切线方程为y=2（x-1），可得：
2a-1=2，解得a=$\frac{3}{2}$．
故选：D．

点评 本题考查导数的运用：求切线的斜率，注意运用直线方程和导数公式，属于基础题．

练习册系列答案
相关题目
15．数列{an}的首项a1=1，{bn}为等比数列且bn=$\frac{{a}_{n+1}}{{a}_{n}}$，若${b_{50}}{b_{51}}={2016^{\frac{1}{50}}}$，则a101=2016．
16．用24个点将一个圆24等分，任意选择其中的三点，则可以组成264个不同的直角三角形．
13．已知f（x）是定义在R上的增函数，函数y=f（x-1）的图象关于点（1，0）对称．若对任意的x，y∈R，不等式f（x2-6x-21）+f（2x）＜0恒成立，x的取值范围是（　　）
A．（-3，7）B．（-9，2）C．（ 3，7）D．（2，9）
20．在项数为n的等差数列{an}中，前三项之和为12，最后三项之和为132，前n项之和为240，则n=10．
10．探究：要使下列事实成立，非零向量$\overrightarrow{a}$，$\overrightarrow{b}$应分别满足什么条件？
（1）$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$共线；
（2）$\overrightarrow{a}$+$\overrightarrow{b}$平分$\overrightarrow{a}$，$\overrightarrow{b}$b所成的角；
（3）|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$$-\overrightarrow{b}$|；
（4）|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|；
（5）|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|．
17．若32x+9=10•3x，则x2+2的值为2或6．
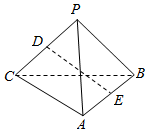14．如图，P是平面ABC外一点，PA=4，BC=2$\sqrt{5}$，D，E分别为PC和AB的中点，且DE=3．求异面直线PA和BC所成角的大小．
15．已知承数f（x）=$\frac{1+μln（x+1）}{λx}$（λ，μ∈R），g（x）=$\frac{k}{x+1}$，若函数f（x）在（1，f（1））处的切线方程为y=-（$\frac{1}{2}$+1n2）x+$\frac{3}{2}$+2ln2．
（1）求λ，μ的值；
（2）求最大的正整数k，?c＞0，?b∈（-1，c），且f（c）=g（b）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网