题目内容
设P是二面角α-l-β内一点,PA⊥平面α,PB⊥平面β,A,B为垂足,且∠APB=60°,则二面角α-l-β的大小为( )
| A、30° | B、60° |
| C、60°或120° | D、120° |
考点:二面角的平面角及求法
专题:空间角
分析:由A作AO⊥l,连结BO,OP,由已知条件推导出P、O、B、A四点共面,∠AOB为二面角α-l-β的平面角,由此能求出二面角α-l-β的大小.
解答:
解:由A作AO⊥l,连结BO,OP
∵PA⊥α于A,OA?α,l?α,
∴PA⊥l,AO⊥l,且AO∩PA=A,
∴l⊥面POA.
∵PA?面POA,∴l⊥P0,
∵PB⊥β于B,l?β,∴PB⊥l,
∵PB∩PO=P,∴l⊥面POB于O,∴l⊥面POA于O.
∵过一点有且只有一个平面垂直于一条直线,∴P、O、B、A四点共面,
且由于OA OB分别包含于面POA和面POB,
∴l⊥OA,l⊥OB,AO∩OB=O,
∴∠AOB为二面角α-l-β的平面角,
∵P在二面角α-l-β内,∴∠APB+∠OBP+∠OAP+∠AOB=360°,
∵∠PAO=∠PBO=90°,∠APB=60°,
∴∠AOB=120°,
故二面角α-l-β为120°.
故选:D.
∵PA⊥α于A,OA?α,l?α,
∴PA⊥l,AO⊥l,且AO∩PA=A,
∴l⊥面POA.
∵PA?面POA,∴l⊥P0,
∵PB⊥β于B,l?β,∴PB⊥l,
∵PB∩PO=P,∴l⊥面POB于O,∴l⊥面POA于O.
∵过一点有且只有一个平面垂直于一条直线,∴P、O、B、A四点共面,
且由于OA OB分别包含于面POA和面POB,
∴l⊥OA,l⊥OB,AO∩OB=O,
∴∠AOB为二面角α-l-β的平面角,
∵P在二面角α-l-β内,∴∠APB+∠OBP+∠OAP+∠AOB=360°,
∵∠PAO=∠PBO=90°,∠APB=60°,
∴∠AOB=120°,
故二面角α-l-β为120°.
故选:D.
点评:本题考查二面角的大小的求法,是中档,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知a、b、c为△ABC的三边,且(a+c)(a-c)=b2+bc,则角A等于( )
| A、150° | B、120° |
| C、60° | D、30° |
三棱锥O-ABC中,OA,OB,OC两两垂直且相等,点P,Q分别是线段BC和OA上移动,且满足BP≤
BC,AQ≤
AO,则PQ和OB所成角余弦值的取值范围是( )
| 1 |
| 2 |
| 1 |
| 2 |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
已知函数y=Asin(ωx+φ)(ω>0)在同一个周期内当x=
时取最大值
,当x=
时取最小值-
,则该函数的解析式为( )
| π |
| 9 |
| 1 |
| 2 |
| 4π |
| 9 |
| 1 |
| 2 |
A、y=2sin(
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=-
|
已知函数y=2sin(ωx+φ)(φ>0)为偶函数(0<φ<π),其图象与直线y=2某两个交点的横坐标分别为x1,x2,若|x1-x2|的最小值为π,则该函数的一个递增区间可以是( )
A、(-
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
若ξ服从正态分布N(10,σ2),若P(ξ<11)=0.9,则P(|ξ-10|<1)=( )
| A、0.1 | B、0.2 |
| C、0.4 | D、0.8 |
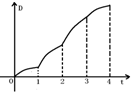
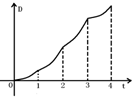
 如图放置的边长为1的正方形PABC沿x轴正方向滚动.设顶点P(x,y)的轨迹方程是y=f(x),设y=f(x)在其两个相邻零点间的图象与x轴所围区域为S,则直线x=t从t=0到t=4所匀速移动扫过区域S的面积D与t的函数图象大致为( )
如图放置的边长为1的正方形PABC沿x轴正方向滚动.设顶点P(x,y)的轨迹方程是y=f(x),设y=f(x)在其两个相邻零点间的图象与x轴所围区域为S,则直线x=t从t=0到t=4所匀速移动扫过区域S的面积D与t的函数图象大致为( )