题目内容
三棱锥O-ABC中,OA,OB,OC两两垂直且相等,点P,Q分别是线段BC和OA上移动,且满足BP≤
BC,AQ≤
AO,则PQ和OB所成角余弦值的取值范围是( )
| 1 |
| 2 |
| 1 |
| 2 |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
考点:异面直线及其所成的角
专题:空间角
分析:如图所示,不妨取OA=2.则B(0,2,0),C(0,0,2).设P(0,y,z),
=λ
,(0≤λ≤
).可得P(0,2-2λ,2λ).设Q(m,0,0),(
≤m≤1).可得cos<
,
>=
=
.对λ,m分类讨论即可得出.
| BP |
| BC |
| 1 |
| 2 |
| 1 |
| 2 |
| PQ |
| OB |
| ||||
|
|
| 1-λ | ||
|
解答:
解:如图所示,不妨取OA=2.则B(0,2,0),C(0,0,2).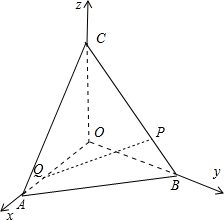
设P(0,y,z),
=λ
,(0≤λ≤
).
则(0,y-2,z)=λ(0,-2,2)=(0,-2λ,2λ),
∴
解得y=2-2λ,z=2λ.
∴P(0,2-2λ,2λ).
设Q(m,0,0),(
≤m≤1).
则
=(m,2λ-2,-2λ),
又
=(0,2,0),
∴cos<
,
>=
=
.
①当点P取B(0,1,0)时,取Q(
,0,0)时,m=
,λ=0,则cos<
,
>=
=
.
取Q(1,0,0)时,m=1,λ=0,cos<
,
>=
.
②当点P取B(0,
,
)时,取Q(
,0,0)时,m=
,λ=
,则cos<
,
>=
=
.
取Q(1,0,0)时,m=1,λ=
,cos<
,
>=
=
.
综上可得:PQ和OB所成角余弦值的取值范围是[
,
].
故选:C.

设P(0,y,z),
| BP |
| BC |
| 1 |
| 2 |
则(0,y-2,z)=λ(0,-2,2)=(0,-2λ,2λ),
∴
|
∴P(0,2-2λ,2λ).
设Q(m,0,0),(
| 1 |
| 2 |
则
| PQ |
又
| OB |
∴cos<
| PQ |
| OB |
| ||||
|
|
| 1-λ | ||
|
①当点P取B(0,1,0)时,取Q(
| 1 |
| 2 |
| 1 |
| 2 |
| PQ |
| OB |
| 1 | ||||
|
2
| ||
| 5 |
取Q(1,0,0)时,m=1,λ=0,cos<
| PQ |
| OB |
| ||
| 2 |
②当点P取B(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PQ |
| OB |
| ||||||
|
| ||
| 3 |
取Q(1,0,0)时,m=1,λ=
| 1 |
| 2 |
| PQ |
| OB |
| ||||
|
| ||
| 6 |
综上可得:PQ和OB所成角余弦值的取值范围是[
| ||
| 6 |
2
| ||
| 5 |
故选:C.
点评:本题考查了向量的夹角公式、异面直线所成的夹角,考查了分类讨论、推理能力和空间想象能力,属于难题.

练习册系列答案
相关题目
设常数a>0,(ax2+
)4的展开式中x3的系数为
,则a=( )
| 1 | ||
|
| 3 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、1 |
不等式-x2+2x+3>0的解集为( )
| A、(-∞,-1)∪(3,+∞) |
| B、(-1,3) |
| C、(-∞,-3)∪(1,+∞) |
| D、(-3,1) |
执行如图的程序框图,若输出的s的值是14,则框图中的n的值是( )


| A、3 | B、4 | C、5 | D、6 |
a=sin
,b=cos
,c=tan
,则a,b,c的大小关系是( )
| 2π |
| 5 |
| 5π |
| 6 |
| 7π |
| 5 |
| A、a>b>c |
| B、c>a>b |
| C、b>a>c |
| D、a>c>b |
已知a>0,b>0且a+2b=2,若
+
>m恒成立,则实数m的取值范围为( )
| 2 |
| a |
| 1 |
| b |
| A、(-∞,8) |
| B、(8,+∞) |
| C、(-∞,4) |
| D、(4,+∞) |
已知2m+n=1,其中m,n均为正数,则
+
的最小值为( )
| 1 |
| m |
| 2 |
| n |
| A、2 | B、4 | C、8 | D、16 |
设P是二面角α-l-β内一点,PA⊥平面α,PB⊥平面β,A,B为垂足,且∠APB=60°,则二面角α-l-β的大小为( )
| A、30° | B、60° |
| C、60°或120° | D、120° |
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中的真命题是( )
| A、若m⊥β,m∥α,则α⊥β |
| B、若m?β,α⊥β,则m⊥α |
| C、若m∥α,n∥β,α∥β,则m∥n |
| D、若m?α,n?β,m∥n,则α∥β |