题目内容
17.已知函数f(x)=mlnx-x2+2(m∈R).(Ⅰ)当m=1时,求f(x)的单调区间;
(Ⅱ)若f(x)在x=1时取得极大值,求证:f(x)-f′(x)≤4x-3;
(Ⅲ)若m≤8,当x≥1时,恒有f(x)-f′(x)≤4x-3恒成立,求m的取值范围.
分析 (Ⅰ)f(x)的定义域为(0,+∞),求出函数的导数,利用f′(x)=0,求出极值点判断函数的单调性,求出单调区间.
(Ⅱ)利用f(x)在x=1时取得极大值,求出m,令g(x)=f(x)-f′(x)-4x+3,通过函数的导数,求出函数的最值即可.
(Ⅲ)令$g(x)=mlnx-{x^2}+2-\frac{m}{x}+2x-4x+3=mlnx-{x^2}-2x-\frac{m}{x}+5$,求出导函数,通过当m≤2时,g′(x)<0,当2<m≤8时,求出g(x)取得最大值.然后求解2≤m≤8.….
解答 (本小题满分14分)
解:(Ⅰ)f(x)的定义域为(0,+∞),$f'(x)=\frac{1}{x}-2x=\frac{{-2{x^2}+1}}{x}$,…(1分)
解f′(x)=0,得$x=±\frac{{\sqrt{2}}}{2}$.当$0<x<\frac{{\sqrt{2}}}{2}$时,f′(x)>0,f(x)单调递增;
当$x>\frac{{\sqrt{2}}}{2}$时,f′(x)<0,f(x)单调递减.…(3分)
综上,当m=1时,f(x)在$({0,\frac{{\sqrt{2}}}{2}})$上单调递增,在$({\frac{{\sqrt{2}}}{2},+∞})$上单调递减.…(4分)
(Ⅱ)若f(x)在x=1时取得极大值,则$\sqrt{\frac{m}{2}}=1$,则m=2.…(5分)
此时f(x)=2lnx-x2+2,$f'(x)=\frac{2}{x}-2x$.
令g(x)=f(x)-f′(x)-4x+3,
则$g(x)=2lnx-{x^2}+2-\frac{2}{x}+2x-4x+3=2lnx-{x^2}-\frac{2}{x}-2x+5$.$g'(x)=\frac{2}{x}-2x+\frac{2}{x^2}-2=\frac{{-2{x^3}-2{x^2}+2x+2}}{x^2}=\frac{{({2x+2})({1-{x^2}})}}{x^2}$.…(6分)
令g′(x)=0,得x=±1.列表得
| x | (0,1) | 1 | (1,+∞) |
| g′(x) | + | 0 | - |
| g(x) | ↗ | 极大值 | ↘ |
由上表知,gmax(x)=g(1)=0,所以g(x)≤0,即f(x)-f′(x)≤4x-3.…(9分)
(Ⅲ)令$g(x)=mlnx-{x^2}+2-\frac{m}{x}+2x-4x+3=mlnx-{x^2}-2x-\frac{m}{x}+5$…(10分)
则$g'(x)=\frac{m}{x}-2x-2+\frac{m}{x^2}=\frac{{-2{x^3}-2{x^2}+mx+m}}{x^2}=\frac{{({x+1})({m-2{x^2}})}}{x^2}$①.
当m≤2时,g′(x)<0,所以g(x)在(1,+∞)上单调递减,所以当x≥1,g(x)≤g(1),
故只需g(1)≤0,即-1-2-m+5≤0,即m≥2,所以m=2.…(12分)
②当2<m≤8时,解g′(x)=0,得$x=±\sqrt{\frac{m}{2}}$.
当$1<x<\sqrt{\frac{m}{2}}$时,g′(x)>0,g(x)单调递增;
当$x>\sqrt{\frac{m}{2}}$时,g′(x)<0,g(x)单调递减.
所以当$x=\sqrt{\frac{m}{2}}$时,g(x)取得最大值.
故只需$g({\sqrt{\frac{m}{2}}})≤0$,即$mln\sqrt{\frac{m}{2}}-\frac{m}{2}-2\sqrt{\frac{m}{2}}-\frac{m}{{\sqrt{\frac{m}{2}}}}+5≤0$,
令$h(x)=xlnx-x-4\sqrt{x}+5$,则$h'(x)=1+lnx-1-\frac{2}{{\sqrt{x}}}=lnx-\frac{2}{{\sqrt{x}}}$,$h''(x)=\frac{1}{x}+\frac{1}{{x\sqrt{x}}}>0$,
所以h′(x)在(1,+∞)上单调递增,
又h′(1)=-2<0,h′(4)=ln4-1>0,以?x0∈(1,4),h′(x0)=0,
所以h(x)在(1,x0)上单调递减,
在(x0,4)上递增,而h(1)=-1-4+5=0,h(4)=4ln4-4-8+5=8ln2-7<0,
所以x∈[1,4]上恒有h(x)≤0,
所以当2<m≤8时,$mln\sqrt{\frac{m}{2}}-\frac{m}{2}-2\sqrt{\frac{m}{2}}-\frac{m}{\sqrt{\frac{m}{2}}}+5≤0$.
综上所述,2≤m≤8.…(14分)
点评 本题考查函数的最值的求法,函数的极值以及函数的单调区间的应用,考查构造法的应用,分析问题解决问题的能力.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. | 3 | B. | 4 | C. | 6 | D. | 2+2$\sqrt{5}$ |
| A. | {0,3} | B. | {-1,0,1,2,3} | C. | {-1,0,3} | D. | {-1,0} |
| A. | 函数y=sinx•cosx的最大值为1 | |
| B. | 将y=sin(2x+$\frac{π}{4}$)图象向右平移$\frac{π}{8}$个单位,再将所得图象上各点的横坐标变为原来的2倍,得到正弦函数y=sinx的图象 | |
| C. | 函数f(x)=1-$\frac{1}{x}$在(-∞,0)上是减函数 | |
| D. | 函数f(x)=$\frac{1}{x}$-x的图象关于y轴对称 |
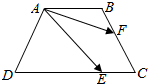 如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$.
如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$.