题目内容
对于项数为m的有穷数列{an},记bk=max{a1,a2,a3,…,ak}(k=1,2,3,…,m),即bk为a1,a2,a3,…,ak中的最大值,则称{bn}是{an}的“控制数列”,{bn}各项中不同数值的个数称为{an}的“控制阶数”.
(Ⅰ)若各项均为正整数的数列{an}的控制数列{bn}为1,3,3,5,写出所有的{an};
(Ⅱ)若m=100,an=tn2-n,其中t∈(
,
),{bn}是{an}的控制数列,试用t表示(b1-a1)+(b2-a2)+(b3-a3)+…+(b100-a100)的值;
(Ⅲ)在1,2,3,4,5的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
(Ⅰ)若各项均为正整数的数列{an}的控制数列{bn}为1,3,3,5,写出所有的{an};
(Ⅱ)若m=100,an=tn2-n,其中t∈(
| 1 |
| 4 |
| 1 |
| 2 |
(Ⅲ)在1,2,3,4,5的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
考点:数列的应用
专题:新定义,等差数列与等比数列
分析:(Ⅰ)若各项均为正整数的数列{an}的控制数列{bn}为1,3,3,5,可得{an};
(Ⅱ)确定当n≥2时,总有an+1>an,n≥3时,总有bn=an.从而只需比较a1和a2的大小,即可得出结论.
(Ⅲ)确定首项为1、2、3、4的数列的个数,即可得出结论.
(Ⅱ)确定当n≥2时,总有an+1>an,n≥3时,总有bn=an.从而只需比较a1和a2的大小,即可得出结论.
(Ⅲ)确定首项为1、2、3、4的数列的个数,即可得出结论.
解答:
解:(Ⅰ)1,3,1,5; 1,3,2,5;1,3,3,5….(3分)
(Ⅱ)因为an=tn2-n,t∈(
,
)
所以
∈(1,2).
所以当n≥2时,总有an+1>an.
又a1=t-1,a3=9t-3.
所以a3-a1=8t-2>0.
故n≥3时,总有bn=an.
从而只需比较a1和a2的大小.
(1)当a1≤a2,即t-1≤4t-2,即t∈[
,
)时,{an}是递增数列,此时bn=an对一切n=1,2,3,…100均成立.
所以(b1-a1)+(b2-a2)+(b3-a3)+…+(b100-a100)=0.
(2)当a1>a2时,即t-1>4t-2,即t∈(
,
)时,b1=a1,b2=a1,bn=an(n≥3).
所以(b1-a1)+(b2-a2)+(b3-a3)+…+(b100-a100)=0+[(t-1)-(4t-2)]+0+…+0=1-3t.
综上,原式=
….(9分)
(Ⅲ)154.
首项为1的数列有6个;
首项为2的数列有6+2=8个;
首项为3的数列有6+4+2=12个;
首项为4的数列有6+6+6+6=24个;
所以,控制阶数为2的所有数列首项之和6+8×2+12×3+24×4=154.…(13分)
(Ⅱ)因为an=tn2-n,t∈(
| 1 |
| 4 |
| 1 |
| 2 |
所以
| 1 |
| 2t |
所以当n≥2时,总有an+1>an.
又a1=t-1,a3=9t-3.
所以a3-a1=8t-2>0.
故n≥3时,总有bn=an.
从而只需比较a1和a2的大小.
(1)当a1≤a2,即t-1≤4t-2,即t∈[
| 1 |
| 3 |
| 1 |
| 2 |
所以(b1-a1)+(b2-a2)+(b3-a3)+…+(b100-a100)=0.
(2)当a1>a2时,即t-1>4t-2,即t∈(
| 1 |
| 4 |
| 1 |
| 3 |
所以(b1-a1)+(b2-a2)+(b3-a3)+…+(b100-a100)=0+[(t-1)-(4t-2)]+0+…+0=1-3t.
综上,原式=
|
(Ⅲ)154.
首项为1的数列有6个;
首项为2的数列有6+2=8个;
首项为3的数列有6+4+2=12个;
首项为4的数列有6+6+6+6=24个;
所以,控制阶数为2的所有数列首项之和6+8×2+12×3+24×4=154.…(13分)
点评:本题考查数列的应用,着重考查分析,对抽象概念的理解与综合应用的能力,对(3)观察,分析寻找规律是难点,是难题.

练习册系列答案
相关题目
如图,在正方体ABCD-A1B1C1D1中,E为BC1的中点,则DE与面BCC1B1所成角的正切值为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )
将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )A、 |
B、 |
C、 |
D、 |
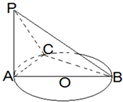 如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )