题目内容
已知sinα=
，α为第二象限的角，则tan2α= ．
| 4 |
| 5 |
考点：二倍角的正切,同角三角函数间的基本关系
专题：三角函数的求值
分析：先求出tanα的值，再由正切函数的二倍角公式可得答案．
解答：
解：因为α为第二象限的角，又sinα=
，所以cosα=-
，
∴tanα=
=-
，
tan2α=
=
，
故答案为：
．
| 4 |
| 5 |
| 3 |
| 5 |
∴tanα=
| sinα |
| cosα |
| 4 |
| 3 |
tan2α=
| 2tanα |
| 1-tan2α |
| 24 |
| 7 |
故答案为：
| 24 |
| 7 |
点评：本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式，同时考查了基本运算能力及等价变换的解题技能．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
如图，在长方形ABCD中，AB=
，BC=1，E为线段DC上一动点，现将△AED沿AE折起，使点D在面ABC上的射影K在直线AE上，当E从D运动到C，则K所形成轨迹的长度为（ ）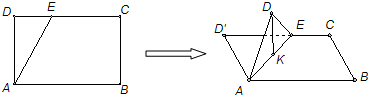
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题正确的是（ ）
| A、若a＞b，则ac2＞bc2 | ||||
| B、若a2＞b2，则a＞b | ||||
C、若
| ||||
D、若
|
已知函数f（x）=-x2-6x-3的单调增区间为（ ）
| A、（-∞，-3] |
| B、[-3，+∞） |
| C、（-∞，3] |
| D、[3，+∞） |
函数y=
的定义域是（ ）
| log2x-2 |
| A、[4，+∞） |
| B、[0，+∞） |
| C、（4，+∞） |
| D、（3，+∞） |