题目内容
函数y=
的定义域是（ ）
| log2x-2 |
| A、[4，+∞） |
| B、[0，+∞） |
| C、（4，+∞） |
| D、（3，+∞） |
考点：对数函数的单调性与特殊点
专题：函数的性质及应用
分析：根据偶次根号下的被开方数大于等于零，对数的真数大于零，列出不等式组，进行求解再用集合或区间的形式表示出来．
解答：
解：要使函数y=
的解析式有意义，
自变量x须满足log2x-2≥0，
即log2x≥2，
即x≥4，
故函数y=
的定义域为[4，+∞），
故选：A
| log2x-2 |
自变量x须满足log2x-2≥0，
即log2x≥2，
即x≥4，
故函数y=
| log2x-2 |
故选：A
点评：本题考查了函数定义域的求法，即根据函数解析式列出使它有意义的不等式组，最后注意要用集合或区间的形式表示出来，这是易错的地方．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
相关题目
与函数y=x相等的函数是（ ）
A、y=（
| |||
B、y=
| |||
C、y=
| |||
D、y=
|
若集合A={x|x2-7x+10＜0}，集合B={x|
＜2x＜8}，则A∩B=（ ）
| 1 |
| 2 |
| A、（-1，3） |
| B、（-1，5） |
| C、（2，5） |
| D、（2，3） |
如图所示程序框图中，某班50名学生，在一次数学考试中，an表示学号为n的学生的成绩，则（ ）
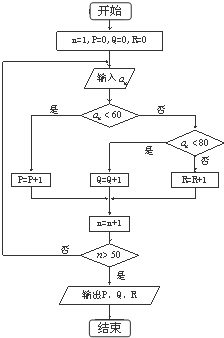
| A、P表示成绩不高于60分的人数 |
| B、Q表示成绩低于80分的人数 |
| C、R表示成绩高于80分的人数 |
| D、Q表示成绩不低于60分，且低于80分人数 |
设函数f（x）=（x2-8x+c1）（x2-8x+c2）（x2-8x+c3） （x2-8x+c4），集合M={x|f（x）=0}={x1，x2…，x7}⊆N+，设c1≥c2≥c3≥c4，则c1-c4（ ）
| A、9 | B、8 | C、7 | D、6 |
若xy≠0，则等式
=-4xy
成立的条件是（ ）
| 16x2y3 |
| y |
| A、x＞0，y＞0 |
| B、x＞0，y＜0 |
| C、x＜0，y＞0 |
| D、x＜0，y＜0 |