题目内容
1.已知函数f(x)=|2x+1|-|x|+a,(1)若a=-1,求不等式f(x)≥0的解集;
(2)若方程f(x)=2x有三个不同的解,求a的取值范围.
分析 (1)通过讨论x的范围,得到关于x的不等式组,解出取并集即可;
(2)求出a=2x+|x|-|2x+1|,令g(x)=2x+|x|-|2x+1|,结合函数的图象求出a的范围即可.
解答  解:(1)当a=-1时,不等式f(x)≥0可化为:|2x+1|-|x|-1≥0,
解:(1)当a=-1时,不等式f(x)≥0可化为:|2x+1|-|x|-1≥0,
∴$\left\{{\begin{array}{l}{x<-\frac{1}{2}}\\{-(2x+1)-(-x)-1≥0}\end{array}}\right.$或$\left\{{\begin{array}{l}{-\frac{1}{2}≤x<0}\\{(2x+1)-(-x)-1≥0}\end{array}}\right.$或$\left\{{\begin{array}{l}{x≥0}\\{(2x+1)-x-1≥0}\end{array}}\right.$,…(3分)
解得:x≤-2或x≥0,…(4分)
∴不等式的解集为(-∞,-2]∪[0,+∞). …(5分)
(2)由f(x)=2x得:a=2x+|x|-|2x+1|,
令g(x)=2x+|x|-|2x+1|,则:$g(x)=\left\{{\begin{array}{l}{3x+{1_{\;}}(x<-\frac{1}{2})}\\{-x-{1_{\;}}(-\frac{1}{2}≤x<0)}\\{x-{1_{\;}}(x≥0)}\end{array}}\right.$,…(7分)
作出函数y=g(x)的图象如图示,
易知$A{(-{\frac{1}{2}_{\;}},-\frac{1}{2})_{\;}},B({0_{\;}},-1)$,
结合图象知:当$-1<a<-\frac{1}{2}$时,函数y=a与y=g(x)的图象有三个不同交点,
即方程f(x)=2x有三个不同的解,…(9分)
∴a的取值范围为$(-{1_{\;}},-\frac{1}{2})$. …(10分)
点评 本题考查了解绝对值不等式问题,考查函数图象的交点问题,是一道中档题.

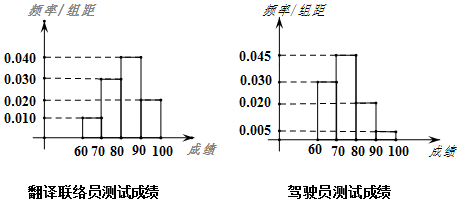
(Ⅰ)能否有90%的把握认为“G20通”与所从事工作(翻译联络员或驾驶员)有关?
(Ⅱ)从参加测试的成绩在80分以上(含80分)的驾驶员中随机抽取4人,4人中“G20通”的人数为随机变量X,求X的分布列与数学期望.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | $\frac{25}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{11}{3}$ | D. | 4 |
| A. | 4 | B. | 0 | C. | 2 | D. | $2\sqrt{10}$ |
| A. | {x|x>-2} | B. | {x|x>2} | C. | {x|0<x<2} | D. | {x|-2<x<2} |
| A. | ¬q | B. | (¬p)∨(¬q) | C. | p∧q | D. | p∧(¬q) |