题目内容
已知等差数列前三项为a,4,3a,前n项的和为Sn
(1)求a;
(2)求
+
+…+
.
(1)求a;
(2)求
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据等差数列的定义和条件,建立方程关系即可得到结论.
(2)求出
的表达式,利用裂项法进行求和.
(2)求出
| 1 |
| Sn |
解答:
解:(1)设该等差数列为{an},
则a1=a,a2=4,a3=3a,
由已知有a+3a=2×4,
解得 a1=a=2,故a=2
(2)由 sn=n•a1+
•d,得 Sn=n(n+1),
=
=
-
,
则
+
+…+
=
+
+…+
=(1-
)+(
-
)+…+(
-
)=1-
则a1=a,a2=4,a3=3a,
由已知有a+3a=2×4,
解得 a1=a=2,故a=2
(2)由 sn=n•a1+
| n(n-1) |
| 2 |
| 1 |
| sn |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则
| 1 |
| s1 |
| 1 |
| s2 |
| 1 |
| sn |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
点评:本题主要考查等差数列的通项公式,以及利用裂项法进行求和,要求熟练掌握常见数列求和的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
α∈[0,2π],且
+
=sinα-cosα,则α∈( )
| 1-cos2α |
| 1-sin2α |
A、[0,
| ||
B、[
| ||
C、[π,
| ||
D、[
|
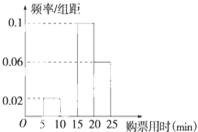 某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的数据(如图所示).
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的数据(如图所示).