Question

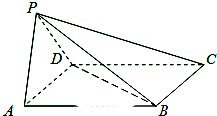如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠BAD=45°，AD=1，AB=

2

，△PAD是正三角形，平面PAD⊥平面PBD．
（Ⅰ）求证：PA⊥BD；
（Ⅱ）求三棱锥P-BCD的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系

专题：空间位置关系与距离

分析：（Ⅰ）要证明PA⊥BD，可以证BD⊥平面PAD，由平面PAD⊥平面PBD，证出PD⊥BD即可；
（Ⅱ）取AD的中点E，连结PE，得PE为三棱锥P-BCD的高；求出高PE，底面积S_△BCD，即得三棱锥P-BCD的体积．

解答： 解：（Ⅰ）证明：由∠BAD=45°，AD=1，AB=

2

，利用余弦定理，可得
BD=

AD2+AB2-2×AD×AB×cos∠BAD

=

12+( 2 )2-2×1× 2 ×cos45°

=1，
∴AD⊥BD；
又∵平面PAD⊥平面PBD，∴BD⊥平面PAD；
又PA?平面PAD，∴PA⊥BD．
（Ⅱ）由（Ⅰ）知BD⊥平面PAD，又BD?平面ABCD，∴平面PAD⊥平面ABCD；
取AD的中点E，连结PE，∵△PAD是正三角形，∴PE⊥AD；
∴PE⊥平面ABCD，即PE为三棱锥P-BCD的高；
在正△PAD中，AD=1，∴PE=

3

2

；
∴三棱锥P-BCD的体积为V=

1

3

×S△BCD×PE=

1

3

×

1

2

×1×1×

3

2

=

3

12

．

点评：本题考查了空间中的线线垂直，线面垂直以及面面垂直问题，也考查了利用垂直关系求锥体的体积问题，是中档题．