题目内容
13.函数f(x)=(${\frac{1}{2}}$)${\;}^{{x^2}-2x+2}}$的值域是( )| A. | (0,$\frac{1}{2}$] | B. | (-∞,$\frac{1}{2}$] | C. | (-∞,2] | D. | [$\frac{1}{2}$,+∞) |
分析 利用配方法求出指数的范围,再由指数函数的单调性求得答案.
解答 解:∵x2-2x+2=(x-1)2+1≥1,
0<(${\frac{1}{2}}$)${\;}^{{x^2}-2x+2}}$$≤\frac{1}{2}$,
∴函数f(x)=(${\frac{1}{2}}$)${\;}^{{x^2}-2x+2}}$的值域是(0,$\frac{1}{2}$].
故选:A.
点评 本题考查与指数函数有关的复合函数的值域的求法,是基础题.

练习册系列答案
相关题目
4.在区间[-1,1]内随机取两个实数x,y,则满足y≥x2的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
1.确定结论“X与Y有关系”的可信度为99.9%时,则随机变量k2的观测值k必须( )
| A. | 大于10.828 | B. | 小于7.829 | C. | 小于6.635 | D. | 大于2.706 |
8.如图,三菱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,则二面角B-PA-C的大小等于( )
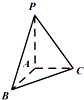

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |