题目内容
3.函数$f(x)={a^{{x^2}-2x-3}}$(a>0,a≠1)有最小值,则不等式loga(x-1)<0的解集为{x|1<x<2}.分析 由复合函数的单调性求得a>1,然后求解对数不等式得答案.
解答 解:函数y=x2-2x-3有最小值,又函数$f(x)={a^{{x^2}-2x-3}}$(a>0,a≠1)有最小值,
∴a>1,
则loga(x-1)<0?loga(x-1)<loga1?0<x-1<1,解得1<x<2.
∴不等式loga(x-1)<0的解集为(1,2).
故答案为:{x|1<x<2}.
点评 本题考查与指数函数有关的复合函数的单调性,考查了对数不等式的解法,是中档题.

练习册系列答案
相关题目
13.函数f(x)=(${\frac{1}{2}}$)${\;}^{{x^2}-2x+2}}$的值域是( )
| A. | (0,$\frac{1}{2}$] | B. | (-∞,$\frac{1}{2}$] | C. | (-∞,2] | D. | [$\frac{1}{2}$,+∞) |
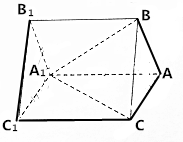 在三棱柱ABC-A1B1C1中已知AB=AC=AA1=2,∠BAA1=∠CAA1=60°,异面直线A1C1与BC成角为45°.
在三棱柱ABC-A1B1C1中已知AB=AC=AA1=2,∠BAA1=∠CAA1=60°,异面直线A1C1与BC成角为45°.