如图.三菱锥P-ABC中.PA⊥平面ABC.∠BAC=90°.则二面角B-PA-C的大小等于( )A．30°B．45°C．60°D．90° 题目和参考答案——青夏教育精英家教网—

题目内容

8．如图，三菱锥P-ABC中，PA⊥平面ABC，∠BAC=90°，则二面角B-PA-C的大小等于（　　）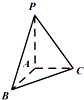

A．

30°

B．

45°

C．

60°

D．

90°

分析由PA⊥平面ABC可得PA⊥AB，PA⊥AC，故∠BAC为所求二面角．

解答解：∵PA⊥平面ABC，AB?平面ABC，AC?平面ABC，
∴PA⊥AB，PA⊥AC，
∴∠BAC为二面角B-PA-C的平面角，
∵∠BAC=90°，
∴二面角B-PA-C为直二面角．
故选D．

点评本题考查了二面角的定义与计算，属于基础题．

练习册系列答案

相关题目

2．

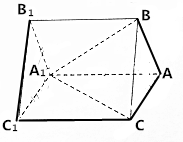在三棱柱ABC-A₁B₁C₁中已知AB=AC=AA₁=2，∠BAA₁=∠CAA₁=60°，异面直线A₁C₁与BC成角为45°．
（1）求证：AA₁⊥BC；
（2）求二面角B-AA₁-C的余弦值；
（3）求直线A₁B于平面A₁AC所成角的正弦值．

19．

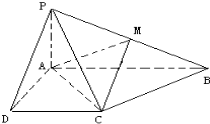已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=$\frac{1}{2}$AB=1，M是PB的中点．
（1）证明：CD⊥面PAD；
（2）求直线AC与PB所成的角；
（3）求点P到平面MAC的距离．

16．判断下列对应哪些是由A到B的映射？为什么？
（1）A=R，B={y|y＞0}，f：x→y=1+$\frac{1}{|x|}$
（2）A=R，B={y|y≥0}，f：x→y=x²
（3）A={x|x≥3}，B={y|y≥0}，f：x→y=$\sqrt{x}$．

3．设数列{a_n}是等差数列，且a₄=-4，a₉=4，S_n是数列{a_n}的前n项和，则（　　）

S₅＜S₆

S₅=S₆

S₇=S₅

S₇=S₆．

13．函数f（x）=（${\frac{1}{2}}$）${\;}^{{x^2}-2x+2}}$的值域是（　　）

20．

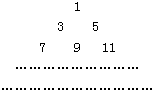把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图三角形数表：
设a_mn（m，n∈N^*）是位于这个三角形数表中从上往下数第m行、从左往右数第n个数．
（1）若a_mn=2017，求m，n的值；
（2）已知函数f（x）=$\frac{{\root{3}{x}}}{2^n}$（x＞0），若记三角形数表中从上往下数第n行各数的和为b_n，求数列{f（b_n）}的前n项和S_n．

17．已知下列随机变量：
①10件产品中有2件次品，从中任选3件，取到次品的件数X；
②一位射击手对目标进行射击，击中目标得1分，未击中目标得0分，用X表示该射击手在一次射击中的得分；
③刘翔在一次110米跨栏比赛中的成绩X；
④在体育彩票的抽奖中，一次摇号产生的号码数X．
其中X是离散型随机变量的是（　　）

18．3名同学分别报名参加学校的足球队，篮球队，乒乓球队，排球队，每人限报其中的一个运动队，不同报法的种数是（　　）

3⁴

4³

试题分类