题目内容
已知等差数列{an}中,公差到d>0,其前n项和为Sn,且满足a2•a3=45,a1+a4=14.
(1)求数列{an}的通项公式;
(2)通过{bn}=
构造一个新的数列{bn},是否存在一个非零常数c,使{bn}也为等差数列;
(3)求f(n)=
(n∈N*)的最大值.
(1)求数列{an}的通项公式;
(2)通过{bn}=
| Sn |
| n+c |
(3)求f(n)=
| bn |
| (n+2005)•bn+1 |
考点:数列与不等式的综合,等差数列的性质
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)利用已知条件结合等差数列的性质列方程组求得a2,a3,则公差可求,代入等差数列的通项公式得答案;
(2)求出等差数列的前n项和,代入bn=
,验证存在一个非零常数c=-
,使{bn}也为等差数列;
(3)把(2)中求出的{bn}的通项公式代入f(n)=
,利用基本不等式放缩,最后作差判断使f(n)求得最大值的n并求得最大值.
(2)求出等差数列的前n项和,代入bn=
| Sn |
| n+c |
| 1 |
| 2 |
(3)把(2)中求出的{bn}的通项公式代入f(n)=
| bn |
| (n+2005)•bn+1 |
解答:
解:(1)∵等差数列{an}中,公差到d>0,且a2•a3=45,a1+a4=14,
∴
,解得
,
∴d=4,
an=a2+4(n-2)=4n-3;
(2)Sn=
=2n(n-
),代入bn=
得,
bn=
,令c=-
,即得bn=2n,
数列{bn}为等差数列,
∴存在一个非零常数c=-
,使{bn}也为等差数列;
(3)f(n)=
=
=
<
,
∵45-
-(
-44)=89-2
=
-
<0,
即45-
<
-44,
∴n=45时,f(n)有最大值
=
.
∴
|
|
∴d=4,
an=a2+4(n-2)=4n-3;
(2)Sn=
| n(1+4n-3) |
| 2 |
| 1 |
| 2 |
| Sn |
| n+c |
bn=
2n(n-
| ||
| n+c |
| 1 |
| 2 |
数列{bn}为等差数列,
∴存在一个非零常数c=-
| 1 |
| 2 |
(3)f(n)=
| bn |
| (n+2005)•bn+1 |
| n |
| (n+2005)(n+1) |
| 1 | ||
n+
|
| 1 | ||
2
|
∵45-
| 2005 |
| 2005 |
| 2005 |
| 7921 |
| 8020 |
即45-
| 2005 |
| 2005 |
∴n=45时,f(n)有最大值
| 45 |
| 2050×46 |
| 9 |
| 18860 |
点评:本题考查了等差数列的性质,考查了等差数列的前n项和,训练了利用基本不等式和放缩法证明数列不等式,是压轴题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
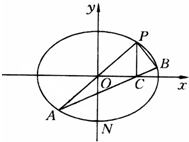 如图,在平面直角坐标系xOy中,过坐标原点的直线交椭圆
如图,在平面直角坐标系xOy中,过坐标原点的直线交椭圆