题目内容
9.已知函数f(x)=[2sin(x+$\frac{π}{3}$)+sinx]cosx-$\sqrt{3}$sin2x(1)求f(x)的周期;
(2)求f(x)在[0,$\frac{5π}{12}$]上的最值.
分析 (1)利用三角函数中的恒等变换可化f(x)=2sin(2x+$\frac{π}{3}$),从而可求其周期;
(2)x∈[0,$\frac{5π}{12}$]⇒2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],利用正弦函数的单调性可求f(x)在[0,$\frac{5π}{12}$]上的最值.
解答 解:(1)原函数可化为:f(x)=(2sinx+$\sqrt{3}$cosx)cosx-$\sqrt{3}$sin2x
=2sinxcosx+$\sqrt{3}$cos2x=2sin(2x+$\frac{π}{3}$),
∴T=$\frac{2π}{2}$=π,
则f(x)的周期为π;
(2)x∈[0,$\frac{5π}{12}$]⇒2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],
∴2sin(2x+$\frac{π}{3}$)∈[-1,2],
∴f(x)在x∈[0,$\frac{5π}{12}$]时,f(x)min=-1,f(x)max=2.
点评 本题考查三角函数中的恒等变换中的应用,考查正弦函数的单调性与最值,属于中档题.

练习册系列答案
相关题目
11. 某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:
某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:
(Ⅰ)在图中画出表中数据的散点图;
(Ⅱ)根据(Ⅰ)中的散点图拟合y与x的回归模型,并用相关系数加以说明;
(Ⅲ)建立y关于x的回归方程,预测第5年的销售量约为多少?.
附注:参考数据:$\sqrt{\sum_{i=1}^4{{{({y_i}-\overline y)}^2}}}≈32.6$,$\sqrt{5}≈2.24$,$\sum_{i=1}^4{{x_i}{y_i}=418}$.
参考公式:相关系数$r=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}\sum_{i=1}^n{{{({y_i}-\overline y)}^2}}}}}$,
回归方程$\widehaty=\widehata+\widehatbx$中斜率和截距的最小二乘法估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
 某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:
某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:| x | 1 | 2 | 3 | 4 |
| y | 12 | 28 | 42 | 56 |
(Ⅱ)根据(Ⅰ)中的散点图拟合y与x的回归模型,并用相关系数加以说明;
(Ⅲ)建立y关于x的回归方程,预测第5年的销售量约为多少?.
附注:参考数据:$\sqrt{\sum_{i=1}^4{{{({y_i}-\overline y)}^2}}}≈32.6$,$\sqrt{5}≈2.24$,$\sum_{i=1}^4{{x_i}{y_i}=418}$.
参考公式:相关系数$r=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}\sum_{i=1}^n{{{({y_i}-\overline y)}^2}}}}}$,
回归方程$\widehaty=\widehata+\widehatbx$中斜率和截距的最小二乘法估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
17.在对人们的休闲方式的一次调查中,共调查 了100人,其中女性55人,男性45人.女性中有40人主要的休闲方式是看电视,另外15人主要的休闲方式是运动;男性中有20人主要休闲方式是看电视,另外25人主要休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表.
(2)是否有99%的把握认为性别与休闲方式有关系?${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(1)根据以上数据建立一个2×2的列联表.
(2)是否有99%的把握认为性别与休闲方式有关系?${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| p(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
14.一个几何体的三视图如图所示,已知这个几何体的体积为$10\sqrt{3}$,则这个几何体的外接球的表面积为( )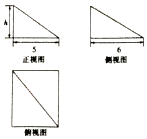

| A. | 8π | B. | 24π | C. | 48π | D. | 64π |
18.已知函数f(x)在R上单调递增,若?x∈R,f(|x+1|)≤f(log2a-|x+2|),则实数a的取值范围是( )
| A. | [2,+∞) | B. | [4,+∞) | C. | [8,+∞) | D. | (0,2] |
5.设z=1-i(i为虚数单位),若复数$\frac{2}{z}$-z2在复平面内对应的向量为$\overrightarrow{OZ}$,则向量$\overrightarrow{OZ}$的模是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
 如图,在正三棱锥A-BCD中,AB=$\sqrt{5}$,点A到底面BCD的距离为1,E为棱BC的中点.
如图,在正三棱锥A-BCD中,AB=$\sqrt{5}$,点A到底面BCD的距离为1,E为棱BC的中点.