题目内容
16.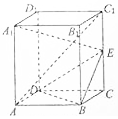 在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证:
在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证:(1)AC1∥平面BDE;
(2)A1E⊥平面BDE.
分析 (1)证明线面平行,只需证明直线与平面内的一条直线平行即可.连接AC与DB交于O,连接OE,AC1∥OE,即可证明AC1∥平面BDE.
(2)证明线面垂直,只需证明直线与平面内的两条相交直线垂直即可.连接OA1,可证OA1⊥DB,OE⊥DB,平面A1OE⊥DB.可得A1E⊥DB.利用勾股定理证明A1E⊥EB即可得A1E⊥平面BDE.
解答 解:(1)ABCD-A1B1C1D1是长方体,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.
可得平面ABCD和平面A1B1C1D1是正方形,E为CC1的中点.
连接AC与DB交于O,连接OE,
可得:AC1∥OE,
OE?平面BDE.
∴AC1∥平面BDE.
(2)连接OA1,
根据三垂线定理,可得OA1⊥DB,OE⊥DB,OA1∩OE=O,
∴平面A1OE⊥DB.
可得A1E⊥DB.
∵E为CC1的中点.设AB=BC=EC=$\frac{1}{2}$AA1=a
∴$BE=\sqrt{2}a$,A1E=$\sqrt{3}a$,A1B=$\sqrt{5}a$
∵A1B2=A1E2+BE2.
∴A1E⊥EB.
∵EB?平面BDE.BD?平面BDE.EB∩BD=B,
∴A1E⊥平面BDE.
点评 本题考查了线面平行,线面垂直的证明.考查学生对书本知识的掌握情况以及空间想象,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
7.空间二直线a,b和二平面α,β,下列一定成立的命题是( )
| A. | 若α⊥β,a⊥b,a⊥α,则b⊥β | B. | 若α⊥β,a⊥b,a⊥α,则b∥β | ||
| C. | 若α⊥β,a∥α,b∥β,则a⊥b | D. | 若α∥β,a⊥α,b?β,则a⊥b |
1.设两点A、B的坐标为A(-1,0)、B(1,0),若动点M满足直线AM与BM的斜率之积为-2,则动点M的轨迹方程为( )
| A. | x2-$\frac{{y}^{2}}{2}$=1 | B. | x2-$\frac{{y}^{2}}{2}$=1(x≠±1) | C. | x2+$\frac{{y}^{2}}{2}$=1 | D. | x2+$\frac{{y}^{2}}{2}$=1(x≠±1) |
5.已知集合M={x|(x+2)(x-3)≤0},N={-3,-1,1,3,5},则M∩N=( )
| A. | {1,3} | B. | {-3,-1,1} | C. | {-3,1} | D. | {-1,1,3} |