题目内容
19.设f(x)=|2x|+|x+a|(I)当a=-1时,求不等式f(x)≤4的解集;
(II)当f(x)=|x-a|时,求x的取值范围.
分析 (I)当a=-1时,$f(x)=\left\{\begin{array}{l}1-3x({x≤0})\\ x+1({0<x≤1})\\ 3x-1({x>1})\end{array}\right.$,即可求不等式f(x)≤4的解集;
(II)当f(x)=|x-a|时,可得2x(x+a)≤0,分类讨论,求x的取值范围.
解答 解:(Ⅰ)$f(x)=\left\{\begin{array}{l}1-3x({x≤0})\\ x+1({0<x≤1})\\ 3x-1({x>1})\end{array}\right.$,
当x≤0时,由f(x)≤4得-1≤x≤0;
当0<x≤1时,由f(x)≤4得0<x≤1;
当x>1时,由f(x)≤4得$1<x≤\frac{5}{3}$;
综上所述,当a=-1时,不等式f(x)≤4的解集为$[{-1,\frac{5}{3}}]$; …(5分)
(Ⅱ)∵f(x)=|2x|+|x+a|≥|2x-(x+a)|=|x-a|,∴2x(x+a)≤0,
当a=0时,x=0;
当a>0时,-a≤x≤0;
当a<0时,0≤x≤-a.…(10分)
点评 本题考查不等式的解法,考查绝对值不等式的性质,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
10.设等差数列{an}的前n项和为Sn,若2a3=3+a1,则S9的值为( )
| A. | 15 | B. | 27 | C. | 30 | D. | 40 |
7.一个几何体的三视图如图所示,则此几何体的体积为( )
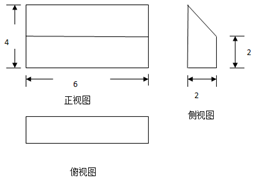

| A. | 16 | B. | 36 | C. | 48 | D. | 72 |
4.在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,E,F,H分别是棱PA,PB,AD的中点,且过E,F,H的平面截四棱锥P-ABCD所得截面面积为$\frac{{3\sqrt{2}}}{2}$,则四棱锥P-ABCD的体积为( )
| A. | $\frac{8}{3}$ | B. | 8 | C. | $8\sqrt{3}$ | D. | $24\sqrt{3}$ |
11.下列选项中说法正确的是( )
| A. | 命题“p∨q为真”是命题“p∧q为真”的必要条件 | |
| B. | 向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}•\overrightarrow{b}>0$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角 | |
| C. | 若am2≤bm2,则a≤b | |
| D. | “?x0∈R,x02-x0≤0”的否定是“?x∈R,x2-x≥0” |