题目内容
已知sinα=
,α∈(
,π),cosβ=-
,β∈(π,
),求sin(α-β),cos(α+β),tan(α+β)的值.
| 2 |
| 3 |
| π |
| 2 |
| 3 |
| 4 |
| 3π |
| 2 |
考点:两角和与差的正弦函数,两角和与差的余弦函数,两角和与差的正切函数
专题:计算题,三角函数的求值
分析:根据已知先求出cosα,sinβ,从而可根据公式依次求出sin(α-β),cos(α+β),tan(α+β)的值.
解答:
解:∵sinα=
,α∈(
,π),∴cosα=-
=-
,
∵cosβ=-
,β∈(π,
),∴sinβ=-
=-
,
∴sin(α-β)=sinαcosβ-cosαsinβ=
×(-
)-(-
)×(-
)=-
,
cos(α+β)=cosαcosβ-sinαsinβ=(-
)×(-
)-
×(-
)=
,
tan(α+β)=
=
=
.
| 2 |
| 3 |
| π |
| 2 |
| 1-sin2α |
| ||
| 3 |
∵cosβ=-
| 3 |
| 4 |
| 3π |
| 2 |
| 1-cos2β |
| ||
| 4 |
∴sin(α-β)=sinαcosβ-cosαsinβ=
| 2 |
| 3 |
| 3 |
| 4 |
| ||
| 3 |
| ||
| 4 |
6+
| ||
| 12 |
cos(α+β)=cosαcosβ-sinαsinβ=(-
| ||
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
| ||
| 4 |
3
| ||||
| 12 |
tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
-
| ||||||||
1-(-
|
27
| ||||
| 17 |
点评:本题主要考察了两角和与差的正弦函数、两角和与差的余弦函数、两角和与差的正切函数公式的应用,计算量比较大,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
(x∈R),则下列结论中不正确的是( )
| x |
| 1+|x| |
| A、对任意x∈R,等式f(-x)+f(x)=0恒成立 |
| B、函数f(x)的值域为(-1,1) |
| C、对任意x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2) |
| D、方程f(x)-x=0则R上有三个根 |
某人午休醒来,发觉表停了,他打开收音机想收听电台整点报时,则他等待的时间短于5分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知某几何本的直观图和三视图如图,则下列判定正确的是( )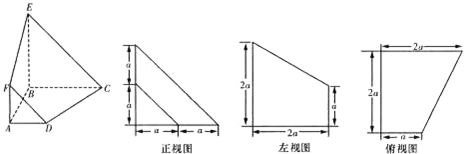

| A、DF∥CE,且BA、CD、EF的延长线不交于同一点 |
| B、DF∥CE,且BA、CD、EF的延长线交于一点 |
| C、DF与CE是异面直线 |
| D、DF与CE相交于一点 |