题目内容
3.已知函数f(x)=|x|,则下列结论正确的是( )| A. | 奇函数,在(-∞,0)上是减函数 | B. | 奇函数,在(-∞,0)上是增函数 | ||
| C. | 偶函数,在(-∞,0)上是减函数 | D. | 偶函数,在(-∞,0)上是增函数 |
分析 去绝对值,根据奇偶性的定义判断即可得答案.
解答 解:函数f(x)=|x|,
则:f(-x)=|-x|=|x|=f(x)
∴函数f(x)是偶函数;
由f(x)=|x|,可得f(x)=$\left\{\begin{array}{l}{x,x≥0}\\{-x,x<0}\end{array}\right.$,根据一次函数的图象可知,f(x)在(-∞,0)上是减函数
∴函数f(x)=|x|是偶函数,在(-∞,0)上是减函数
故选C.
点评 本题主要考查了函数的奇偶性的定义域判断和单调性的判断.属于基础题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
13.已知函数f(x)=Asin(ωx+φ)+B,(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,则( )
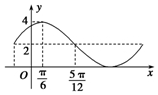

| A. | A=4 | B. | ω=1 | C. | φ=$\frac{π}{6}$ | D. | B=4 |
14.已知点M(-2,2)在抛物线C:y2=2px(p>0)的准线上,记抛物线C的焦点为F,则直线MF的方程为( )
| A. | x-2y+6=0 | B. | x+2y-2=0 | C. | 2x-y+6=0 | D. | 2x+y+2=0 |
11.若sinα>0且tanα<0,则$\frac{α}{2}$的终边在( )
| A. | 第一象限 | B. | 第二象限 | ||
| C. | 第一象限或第三象限 | D. | 第三象限或第四象限 |
18.在空间中,已知$\overrightarrow{AB}$=(2,4,0),$\overrightarrow{DC}$=(-1,3,0),则异面直线AB与DC所成角θ的大小为( )
| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
8.设(1+i)(x+yi)=2,其中x,y是实数,则|2x+yi|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
13.p:x>1,q:x>0,则p是q的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |