题目内容
2.cos1200°=( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
分析 原式中的角度变形后,利用诱导公式及特殊角的三角函数值计算即可得到结果.
解答 解:原式=cos(3×360°+120°)=cos120°=-cos60°=-$\frac{1}{2}$,
故选:B.
点评 此题考查了运用诱导公式化简求值,以及特殊角的三角函数值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
12.在我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(“倍加增”指灯的数量从塔的顶层到底层按公比为2的等比数列递增).根据此诗,可以得出塔的顶层和底层共有( )
| A. | 3盏灯 | B. | 192盏灯 | C. | 195盏灯 | D. | 200盏灯 |
13.若0<a<b<1,c>1,则( )
| A. | ac>bc | B. | abc>bac | C. | logab>logba | D. | logac<logbc |
10.已知p>0,q>0,随机变量ξ的分布列如下:
若E(ξ)=$\frac{4}{9}$.则p2+q2=( )
| ξ | p | q |
| P | q | p |
| A. | $\frac{4}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{9}$ | D. | 1 |
17.一个几何体的三视图如图所示(三个正方形的边长都是2),则该几何体的表面积是( )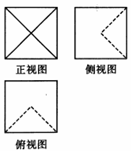

| A. | $20+4\sqrt{2}$ | B. | $24+4\sqrt{2}$ | C. | 24 | D. | 28 |
16.已知i为虚数单位,复数$z={(\frac{i-1}{i+1})^3}$,则z=( )
| A. | -i | B. | i | C. | 1+i | D. | -1+i |