题目内容
9.如果x=[x]+{x},[x]∈Z,0≤{x}<1,就称[x]表示x的整数部分,{x}表示x的小数部分.已知数列{an}满足a1=$\sqrt{5}$,an+1=[an]+$\frac{1}{\{{a}_{n}\}}$,则a2017等于( )分析 由已知求出数列的前四项,从而猜想an=4(n-1)+$\sqrt{5}$,由此能求出结果.
解答 解:∵${a}_{1}=\sqrt{5}$,an+1=[an]+$\frac{1}{\{{a}_{n}\}}$,
∴a2=2+$\frac{1}{\sqrt{5}-2}$=4+$\sqrt{5}$,
${a}_{3}=6+\frac{1}{\sqrt{5}-2}$=8+$\sqrt{5}$,
a4=10+$\frac{1}{\sqrt{5}-2}$=12+$\sqrt{5}$,
${a}_{5}=14+\frac{1}{\sqrt{5}-2}$=16+$\sqrt{5}$,
…
∴an=4(n-1)+$\sqrt{5}$,
∴a2017=4×2016+$\sqrt{5}$=8064+$\sqrt{5}$.
点评 解决该试题的关键是对于两个数列通项公式的分析和求解,然后能合理的选用求公式来得到结论.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
4.函数y=$\frac{1}{{x}^{2}-4x+3}$(x≠1且x≠3)的值域为( )
| A. | [$\frac{1}{3}$,+∞) | B. | [-1,0)∪(0,+∞) | C. | [-1,+∞) | D. | (-∞,-1]∪(0,+∞) |
14.若一圆弧长等于它所在圆的内接正三角形的边长,则该弧所对的圆心角弧度数为( )
| A. | $\frac{π}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{2π}{3}$ | D. | 2 |
3.若0<a<1,b<-1,则函数f(x)=ax+b的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
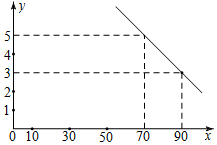 近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为40元,经销过程中测出年销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售这种口罩的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.
近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为40元,经销过程中测出年销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售这种口罩的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.