题目内容
4.函数y=$\frac{1}{{x}^{2}-4x+3}$(x≠1且x≠3)的值域为( )| A. | [$\frac{1}{3}$,+∞) | B. | [-1,0)∪(0,+∞) | C. | [-1,+∞) | D. | (-∞,-1]∪(0,+∞) |
分析 结合二次函数的图象和性质,分析出分母的取值范围,进而可得函数y=$\frac{1}{{x}^{2}-4x+3}$(x≠1且x≠3)的值域.
解答 解:∵x2-4x+3≥-1,
当x≠1且x≠3时,x2-4x+3≠0,
故x2-4x+3∈[-1,0)∪(0,+∞),
故函数y=$\frac{1}{{x}^{2}-4x+3}$(x≠1且x≠3)的值域为(-∞,-1]∪(0,+∞),
故选:D
点评 本题考查的知识点是二次函数的图象和性质,函数的值域,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.椭圆的两个焦点分别为F1(-1,0)和F2(1,0),若该椭圆与直线x+y-3=0有公共点,则其离心率的最大值为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{6}}}{6}$-1 | C. | $\frac{{\sqrt{6}}}{12}$ | D. | $\frac{{\sqrt{5}}}{10}$ |
12.若将函数f(x)=$\frac{1}{2}$sin(2x+$\frac{π}{3}$)图象上的每一个点都向左平移$\frac{π}{3}$个单位,得到g(x)的图象,则函数g(x)的单调递增区间为( )
| A. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) | B. | [kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$](k∈Z) | ||
| C. | [kπ-$\frac{2π}{3}$,kπ-$\frac{π}{6}$](k∈Z) | D. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) |
16.设向量$\vec a=(1,-1)$,$\vec b=(-1,2)$,则$(2\overrightarrow a+\overrightarrow b)•\overrightarrow a$=1.
18.“a>b”是“a2>b2”的__________条件( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
 已知${a_n}=2n(n∈{N^*})$,把数列{an}的各项按如图的规律排成一个三角形数阵,记F(p,q)表示第p行从左至右的第q个数,则F(8,6)的值为110.
已知${a_n}=2n(n∈{N^*})$,把数列{an}的各项按如图的规律排成一个三角形数阵,记F(p,q)表示第p行从左至右的第q个数,则F(8,6)的值为110.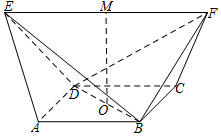 如图,在五面体ABCDEF中,底面ABCD是正方形,△ADE,△BCF都是等边三角形,EF∥AB,且EF>AB,M,O分别为EF,BD的中点,连接MO.
如图,在五面体ABCDEF中,底面ABCD是正方形,△ADE,△BCF都是等边三角形,EF∥AB,且EF>AB,M,O分别为EF,BD的中点,连接MO.