题目内容
9.已知函数f(x)=$\sqrt{2}$sin(2ωx+φ)(x∈R),其中ω>0,|φ|<$\frac{π}{2}$,f(x)满足以下两个条件:①两条相邻对称轴之间的距离为π;②f(0)=1.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)在[0,π]内的单调递增区间;
(Ⅲ)若方程f(x)+a=0在$[{0,\;\frac{5π}{8}}]$内有2个不等实根,求实数a的取值范围.
分析 (Ⅰ)由周期求出ω,有特殊点的坐标求出φ,可得函数的解析式.
(Ⅱ)由条件利用正弦函数的单调性求得函数f(x)在[0,π]内的单调递增区间.
(Ⅲ)由题意利用函数的单调性求得函数的值域,可得a的范围.
解答 解:(Ⅰ)∵T=$\frac{2π}{ω}$=2π,所以ω=1,∴函数f(x)=$\sqrt{2}$sin(2x+φ).
又f(0)=$\sqrt{2}$sinφ=1,∴sinφ=$\frac{\sqrt{2}}{2}$,结合|φ|<$\frac{π}{2}$,可得φ=$\frac{π}{4}$.
∴$f(x)=\sqrt{2}sin({2x+\frac{π}{4}})$.
(Ⅱ)令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,得 kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$,k∈Z,
故函数的增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.
又因为0≤x≤π,函数f(x)在[0,π]内的单调递增区间为[0,$\frac{π}{8}$]和[$\frac{5π}{8}$,π].
(Ⅲ)由题意知:函数y=f(x)与y=-a图象在$[{0,\;\frac{5π}{8}}]$内有两个交点,
由(Ⅱ)可知函数f(x)在[0,$\frac{π}{8}$]上是增函数,在$[{\frac{π}{8},\;\frac{5π}{8}}]$上是减函数.
又f(0)=1,$f({\frac{π}{8}})=\sqrt{2}$,$f({\frac{5π}{8}})=-\sqrt{2}$,所以$1≤-a<\sqrt{2}$,即$-\sqrt{2}<a≤1$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的单调性,正弦函数的图象特征,正弦函数的定义域和值域,属于中档题.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | (0,1) | B. | (0,$\frac{1}{2}$) | C. | (-∞,2) | D. | (-∞,1) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{3}{20}$ | B. | $\frac{13}{100}$ | C. | $\frac{3}{25}$ | D. | $\frac{7}{50}$ |
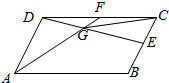 如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)
如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)