题目内容

12．在数列{xn}中，x1=8，x4=2，且满足xn+2+xn=2xn+1，n∈N+．则x10=（　　）
A．-10B．10C．-20D．20

分析 由数列递推式可知数列{xn}是等差数列，由已知求得公差，代入等差数列的通项公式得答案．

解答 解：由足xn+2+xn=2xn+1，n∈N+．
可知数列{xn}是等差数列，又x1=8，x4=2，
则公差d=$\frac{{x}_{4}-{x}_{1}}{4-1}=\frac{2-8}{3}=-2$．
∴x10=x1+9d=8+9×（-2）=-10．
故选：A．

点评 本题考查数列递推式，考查了等差关系的确定，是基础题．

练习册系列答案
相关题目
2．正方形ABCD的边长为4，E，F分别是AB，AD的中点，PC⊥面ABCD，PC=2，求点B到平面PEF的距离．
3．函数y=$\frac{2}{x}$的单调减区间为（　　）
A．RB．（-∞，0）∪（0，+∞）C．（-∞，0），（0，+∞）D．（0，+∞）
20．在直角坐标平面内，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosa}\\{y=2+2sina}\end{array}\right.$（a为参数），直线l的极坐标方程为ρcos（θ-$\frac{π}{6}$）=2．
（1）分别求出曲线C和直线l的直角坐标方程；
（2）若点P在曲线C上，且点P到直线l的距离为1，求满足这样条件的点P的个数．
7．在空间平移△ABC到△A1B1C1（使△A1B1C1与△ABC不共面），连接对应顶点，设$\overrightarrow{A{A}_{1}}$=$\overrightarrow{a}$，$\overrightarrow{AB}$=$\overrightarrow{b}$，$\overrightarrow{AC}$=$\overrightarrow{c}$，M是BC1的中点，N是B1C1的中点，用基底{$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$}表示向量$\overrightarrow{AM}$+$\overrightarrow{AN}$的结果是$\frac{3}{2}$$\overrightarrow{a}$$+\overrightarrow{b}$$+\overrightarrow{c}$．
17．点A（sin1，cos1）在直角坐标平面上位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
4．设函数f（x）是奇函数，并且在R上为增函数，若0≤θ≤$\frac{π}{6}$时，f（msinθ）+f（1-m）＞0恒成立，则实数m的取值范围是（　　）
A．（0，1）B．（0，$\frac{1}{2}$）C．（-∞，2）D．（-∞，1）
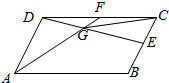1．如图，已知E，F分别是平行四边形ABCD的边BC，CD中点，AF与DE相交于点G，若$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$（用$\overrightarrow{a}$，$\overrightarrow{b}$表示）
2．设f（x）=（x-1）3+x+2，{an}是公差为$\frac{1}{2}$的等差数列，且f（a1）+f（a2）+f（a3）+f（a4）+f（a5）+f（a6）=18，则a1=（　　）
A．-$\frac{1}{4}$B．-$\frac{7}{4}$C．-$\frac{5}{4}$D．-$\frac{3}{4}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网