题目内容
7．
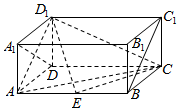如图，在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动．（1）证明：BC1∥平面ACD1．
（2）当$AE=\frac{1}{4}AB$时，求三棱锥E-ACD1的体积．
分析 （1）根据四边形ABC1D1是平行四边形得出AD1∥BC1，于是BC1∥平面ACD1．
（2）以△ACE为棱锥的底面，则棱锥的高为DD1，代入棱锥的体积公式计算．
解答 （1）证明：∵AB∥C1D1，AB=C1D1，
∴四边形ABC1D1是平行四边形，
∴BC1∥AD1，
又∵AD1?平面ACD1，BC1?平面ACD1，
∴BC1∥平面ACD1．
（2）解：S△ACE=$\frac{1}{2}$AE•AD=$\frac{1}{2}×\frac{1}{2}×1$=$\frac{1}{4}$．
∴V${\;}_{E-AC{D}_{1}}$=V${\;}_{{D}_{1}-ACE}$=$\frac{1}{3}{S}_{△ACE}•D{D}_{1}$=$\frac{1}{3}×\frac{1}{4}×1$=$\frac{1}{12}$．
点评 本题考查了线面平行的判定，长方体的结构特征，棱锥的体积计算，属于中档题．
练习册系列答案
金钥匙试卷系列答案
相关题目
14．若a=20.5，b=1og21.3，c=log2sin$\frac{2π}{5}$，则（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞a＞b | D． | b＞c＞a |
18．若α，β都是锐角，且$sinα=\frac{2\sqrt{5}}{5}，sin（α-β）=\frac{\sqrt{10}}{10}$，则cosβ=（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{10}$ | C． | $\frac{\sqrt{2}}{2}$或$-\frac{\sqrt{2}}{10}$ | D． | $\frac{\sqrt{2}}{2}$或$\frac{\sqrt{2}}{10}$ |
2．$cos\frac{2π}{3}•tan\frac{7π}{4}$的值为（ ）
| A． | $-\frac{1}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
如图，在正四棱锥P-ABCD中，PA=AB=2，点E在棱PC上．