题目内容
17.已知函数$f(x)=\left\{\begin{array}{l}{log_2}(x+3),x≥0\\{x^2},x<0\end{array}\right.$则f(f(-1))=2.分析 根据分段函数的表达式,利用代入法进行求解即可.
解答 解:由分段函数的表达式得f(-1)=(-1)2=1,
则f(1)=log2(1+3)=log24=2,
f(f(-1))=f(1)=2,
故答案为:2
点评 本题主要考查函数值的计算,根据分段函数的表达式,利用代入法是解决本题的关键.比较基础.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
8.用一个平面去截一个所有棱长均为1的五棱锥,其截面图形不可能是( )
| A. | 钝角三角形 | B. | 等腰梯形 | C. | 平行四边形 | D. | 正五边形 |
12.班集体搞某项活动,将全班同学分成3个不同的小组,每位同学被分到每个小组的可能性相同,则甲、乙两位同学被分到同一个小组的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
2.执行如图的程序框图,若输入n=3,则输出的S=( )
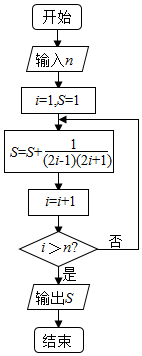

| A. | $\frac{3}{7}$ | B. | $\frac{8}{7}$ | C. | $\frac{10}{7}$ | D. | $\frac{13}{7}$ |
9.复数z(1+i)=2i,则z的共轭复数为( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |
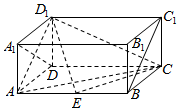 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.