题目内容
15.一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是$({1,0,\frac{1}{2}}),({1,1,0}),({0,\frac{1}{2},1})({1,0,1})$,画该四面体三视图中的正视图时,以yOz平面为投影面,则得到的正视图可以为( )| A. | 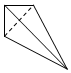 | B. | 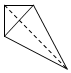 | C. | 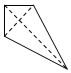 | D. | 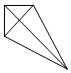 |
分析 根据题意,在空间直角坐标系下画出空间四面体ABCD的图形,并且写出四面体在yOz平面的投影点,由此得到正视图的图形.
解答  解:根据题意,在空间直角坐标系下画出空间四面体ABCD的图形,如图所示,
解:根据题意,在空间直角坐标系下画出空间四面体ABCD的图形,如图所示,
则该四面体在yOz平面的投影是点(0,0,$\frac{1}{2}$),
(0,1,0),(0,$\frac{1}{2}$,1),(0,0,1)组成的平面图形,
所以正视图是A所示的图形.
故选:A.
点评 本题考查了空间几何体三视图的应用问题,也考查了几何投影的应用问题,是基础题目.

练习册系列答案
相关题目
6.在△ABC中,若$BC=\sqrt{3}$,$AC=\sqrt{2}$,∠B=45°,则∠A=( )
| A. | 60°或120° | B. | 60° | C. | 30°或150° | D. | 30° |
20.已知直线l的倾斜角为α,且60°<α≤135°,则直线l斜率的取值范围是( )
| A. | $(\sqrt{3},+∞)$ | B. | $[-1,\sqrt{3})$ | C. | $(-∞,-1]∪(\sqrt{3},+∞)$ | D. | $(-∞,-1)∪[\sqrt{3},+∞)$ |
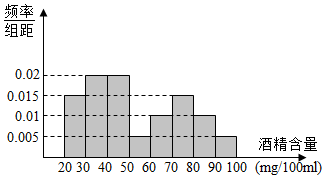 按规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含90)之间,属酒后驾车;在80mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.
按规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含90)之间,属酒后驾车;在80mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.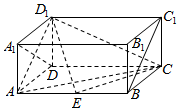 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.