题目内容
从2009名学生中选取50名学生参加数学竞赛，若采用下面的方法选取：先用简单随机抽样从2009人中剔除9人，剩下的2000人再按系统抽样的方法抽取50人，则在2009人中，每人入选的概率（ ）
| A、不全相等 | ||
| B、均不相等 | ||
C、都相等，且为
| ||
D、都相等，且为
|
考点：相互独立事件的概率乘法公式
专题：计算题,概率与统计
分析：在系统抽样中，若所给的总体个数不能被样本容量整除，则要先剔除几个个体，然后再分组，在剔除过程中，每个个体被剔除的概率相等，每个个体被抽到包括两个过程，这两个过程是相互独立的．
解答：
解：∵在系统抽样中，若所给的总体个数不能被样本容量整除，则要先剔除几个个体，然后再分组，
在剔除过程中，每个个体被剔除的概率相等，
∴每个个体被抽到包括两个过程，一是不被剔除，二是选中，这两个过程是相互独立的，
∴每人入选的概率p=
×
=
，
故选C．
在剔除过程中，每个个体被剔除的概率相等，
∴每个个体被抽到包括两个过程，一是不被剔除，二是选中，这两个过程是相互独立的，
∴每人入选的概率p=
| 2000 |
| 2009 |
| 50 |
| 2000 |
| 50 |
| 2009 |
故选C．
点评：在系统抽样过程中，为将整个的编号分段（即分成几个部分），要确定分段的间隔，当在系统抽样过程中比值不是整数时，通过从总体中删除一些个体（用简单随机抽样的方法）．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
学校为了了解高二年级教学情况，对全省班、实验班、普通班、中加班的学生做分层抽样调查．假设我校高二年级总人数为N，其中全省班有学生96人．若在全省班、实验班、普通班、中加班抽取的人数分别为12，21，25，43，则总人数N为（ ）
| A、801 | B、808 |
| C、853 | D、912 |
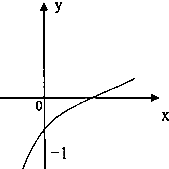
已知函数f（x）=loga（2x+b-1）（a＞0且a≠1）的图象如图所示，则a、b满足的关系式是（ ）
A、0＜b＜
| ||||
B、0＜
| ||||
C、0＜
| ||||
D、0＜
|
下列四个命题中正确的有（ ）
①函数y=x -
的定义域是{x|x≠0}；
②方程lg
=lg（x-2）的解集为{3}；
③不等式lg（x-1）＜1的解集是{x|x＜11}
④方程31-x-2=0的解集为{x|x=1-log32}．
①函数y=x -
| 1 |
| 2 |
②方程lg
| x-2 |
③不等式lg（x-1）＜1的解集是{x|x＜11}
④方程31-x-2=0的解集为{x|x=1-log32}．
| A、①② | B、②③④ | C、①③ | D、②④ |
直线l过点P（-2，0）且与圆x2+y2=1相切，则l的斜率是（ ）
| A、±1 | ||||
B、±
| ||||
C、±
| ||||
D、±
|
已知函数f（x）=
（x＞0），则函数y=f（x）的值域是（ ）
| x-1 |
| x+1 |
| A、[-1，1] |
| B、（-1，1] |
| C、（-1，1） |
| D、以上都不对 |
以正方体的顶点为顶点的三棱锥的个数是（ ）
| A、70 | B、64 | C、60 | D、58 |
函数y=x2-6x+1，x∈[2，5]的值域是（ ）
| A、[-8，-4] |
| B、[-8，-4） |
| C、[-7，-4] |
| D、[-7，-4） |