题目内容

方程2012x+2013x+2014x=2015x
x-2016
的实根个数为（　　）
A、0个B、1个
C、2个D、至少3个
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：方程2012x+2013x+2014x=2015x
x-2016
的实根，即方程(
2012
2015
)x+(
2013
2015
)x+(
2014
2015
)x=
x-2016
的实根，即方程(
2012
2015
)x+(
2013
2015
)x+(
2014
2015
)x-
x-2016
=0的实根，令f（x）=(
2012
2015
)x+(
2013
2015
)x+(
2014
2015
)x-
x-2016
，利用零点存在定理分析函数零点的个数，进而可得答案．
解答： 解：方程2012x+2013x+2014x=2015x
x-2016
的实根，
即方程(
2012
2015
)x+(
2013
2015
)x+(
2014
2015
)x=
x-2016
的实根，
即方程(
2012
2015
)x+(
2013
2015
)x+(
2014
2015
)x-
x-2016
=0的实根，
令f（x）=(
2012
2015
)x+(
2013
2015
)x+(
2014
2015
)x-
x-2016
，
由y=(
2012
2015
)x+(
2013
2015
)x+(
2014
2015
)x为减函数，y=
x-2016
为增函数，
故f（x）=(
2012
2015
)x+(
2013
2015
)x+(
2014
2015
)x-
x-2016
在[2016，+∞）为减函数，
又∵f（2006）＞0，f（2007）＜0，
故函数f（x）=(
2012
2015
)x+(
2013
2015
)x+(
2014
2015
)x-
x-2016
有且只有一个零点，
即方程2012x+2013x+2014x=2015x
x-2016
的实根个数为1个，
故选：B
点评：本题考查的知识点是根的存在性及根的个数判断，熟练掌握方程根的个数与函数零点的关系，及函数零点的存在定理是解答的关键．
练习册系列答案
相关题目
若函数f（x）=x2+ax（a＞0）对区间（
1
2
，1）内的任意两个相异的实数x1，x2恒有|f（x1）-f（x2）|＞2|x1-x2|，则实数a的取值范围是
 
．
下列命题：
①偶函数的图象一定与y轴相交；
②任取x＞0，均有（
1
2
）x＞（
1
3
）x；
③在同一坐标系中，y=log2x与y=log
1
2
x的图象关于x轴对称；
④A=R，B=R，f：x→y=
1
x+1
，则f为A到B的映射；
⑤y=
1
x
在（-∞，0）∪（0，+∞）上是减函数．
其中正确的命题的序号是
 
．
已知条件p：x≠1或y≠2，条件q：xy≠2，那么￢p是￢q的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
已知a=π 
1
3
，b=logπ3，c=log3
π
3
，则a，b，c大小关系为（　　）
A、a＞b＞c
B、b＞c＞a
C、c＞a＞b
D、c=a＞b
已知a，b为正实数，函数f（x）=ax3+bx+2在[0，1]上的最大值为4，则f（x）在[-1，0]上的最小值为（　　）
A、0
B、
3
2
C、-2
D、2
学校为了了解高二年级教学情况，对全省班、实验班、普通班、中加班的学生做分层抽样调查．假设我校高二年级总人数为N，其中全省班有学生96人．若在全省班、实验班、普通班、中加班抽取的人数分别为12，21，25，43，则总人数N为（　　）
A、801B、808
C、853D、912
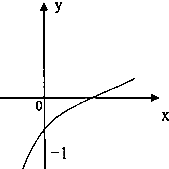
已知函数f（x）=loga（2x+b-1）（a＞0且a≠1）的图象如图所示，则a、b满足的关系式是（　　）
A、0＜b＜
1
a
＜1
B、0＜
1
a
＜b＜1
C、0＜
1
b
＜a＜1
D、0＜
1
a
＜
1
b
＜1
以正方体的顶点为顶点的三棱锥的个数是（　　）
A、70B、64C、60D、58

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网