题目内容
在(
-x2)6的展开式中,x3的系数是 (用数字作答).
| 1 |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x的幂指数等于3,求得r的值,即可求得展开式的x3项的系数.
解答:
解:二项式(
-x2)6=(x2-
)6展开式的通项公式为Tr+1=
•x12-2r•(-1)r•x-r=(-1)r
•x12-3r,
令12-3r=3,解得r=3,故二项式(x2-
)6展开式中的x3项的系数为-1×20=-20,
故答案为:-20.
| 1 |
| x |
| 1 |
| x |
| C | r 6 |
| C | r 6 |
令12-3r=3,解得r=3,故二项式(x2-
| 1 |
| x |
故答案为:-20.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知g(x)=ax+a,f(x)=
,对?x1∈[-2,2],?x2∈[-2,2],使g(x1)=f(x2)成立,则a的取值范围是( )
|
| A、[-1,+∞) |
| B、[-1,1] |
| C、(0,1] |
| D、(-∞,1] |
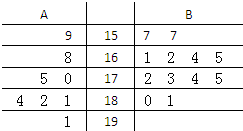 某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.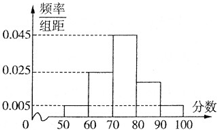 某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分…第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有
某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分…第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有