题目内容
已知等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6
(1)求数列{an}的通项公式
(2)设bn=log3a1+log3a2+…+log3an,求{bn}的通项公式.
(1)求数列{an}的通项公式
(2)设bn=log3a1+log3a2+…+log3an,求{bn}的通项公式.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)设出等比数列的公比q,由a32=9a2a6,利用等比数列的通项公式化简后得到关于q的方程,由已知等比数列的各项都为正数,得到满足题意q的值,然后再根据等比数列的通项公式化简2a1+3a2=1,把求出的q的值代入即可求出等比数列的首项,根据首项和求出的公比q写出数列的通项公式即可;
(Ⅱ)把(Ⅰ)求出数列{an}的通项公式代入设bn=log3a1+log3a2+…+log3an,利用对数的运算性质及等差数列的前n项和的公式化简后,即可得到bn的通项公式,求出倒数即为
的通项公式,然后根据数列的通项公式列举出数列的各项,抵消后即可得到数列{
}的前n项和.
(Ⅱ)把(Ⅰ)求出数列{an}的通项公式代入设bn=log3a1+log3a2+…+log3an,利用对数的运算性质及等差数列的前n项和的公式化简后,即可得到bn的通项公式,求出倒数即为
| 1 |
| bn |
| 1 |
| bn |
解答:
解:(Ⅰ)设数列{an}的公比为q,由a32=9a2a6得a32=9a42,所以q2=
.
由条件可知各项均为正数,故q=
.
由2a1+3a2=1得2a1+3a1q=1,所以a1=
.
故数列{an}的通项式为an=
.
(Ⅱ)bn=log3a1+log3a2+…+log3an,
故
=-
=-2(
-
)
则
+
+…+
=-2[(1-
)+(
-
)+…+(
-
)]=-
,
所以数列{
}的前n项和为-
.
| 1 |
| 9 |
由条件可知各项均为正数,故q=
| 1 |
| 3 |
由2a1+3a2=1得2a1+3a1q=1,所以a1=
| 1 |
| 3 |
故数列{an}的通项式为an=
| 1 |
| 3n |
(Ⅱ)bn=log3a1+log3a2+…+log3an,
故
| 1 |
| bn |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 2n |
| n+1 |
所以数列{
| 1 |
| bn |
| 2n |
| n+1 |
点评:此题考查学生灵活运用等比数列的通项公式化简求值,掌握对数的运算性质及等差数列的前n项和的公式,会进行数列的求和运算,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
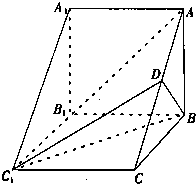 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,A1A=AB=2.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,A1A=AB=2.