题目内容
已知二次函数f(x)=ax2+bx+c,满足对称轴x=-
,且f(x)<2x的解集为(-1,
),求f(x).
| 1 |
| 4 |
| 3 |
| 2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:由对称轴得到a,b的关系式,由f(x)<2x的解集为(-1,
),得到f(x)=2x的两根分别为-1,
,利用根与系数的关系得到系数的方程组解之即可.
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:∵二次函数f(x)=ax2+bx+c,满足对称轴x=-
,且f(x)<2x的解集为(-1,
),
∴-
=-
①
f(x)=2x即ax2+(b-2)x+c=0的两根分别为-1,
,
∴-1+
=
②
-1×
=
③
①②③组成方程组解得a=2,b=1,c=-3,
∴f(x)=2x2+x-3.
| 1 |
| 4 |
| 3 |
| 2 |
∴-
| b |
| 2a |
| 1 |
| 4 |
f(x)=2x即ax2+(b-2)x+c=0的两根分别为-1,
| 3 |
| 2 |
∴-1+
| 3 |
| 2 |
| 2-b |
| a |
-1×
| 3 |
| 2 |
| c |
| a |
①②③组成方程组解得a=2,b=1,c=-3,
∴f(x)=2x2+x-3.
点评:本题考查了二次函数的性质以及一元二次不等式的解集与对应一元二次方程的根之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
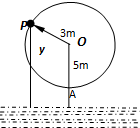 如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=
如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=