题目内容
先解答(1),再通过结构类比解答(2):
(1)求证:tan(x+
)=
;
(2)设x∈R,a为非零常数,且f(x+a)=
,试问:f(x)是周期函数吗?证明你的结论.
(1)求证:tan(x+
| π |
| 4 |
| 1+tanx |
| 1-tanx |
(2)设x∈R,a为非零常数,且f(x+a)=
| 1+f(x) |
| 1-f(x) |
考点:两角和与差的正切函数,类比推理
专题:三角函数的图像与性质
分析:(1)直接利用两角和的正切函数化简求解即可.
(2)猜想是周期函数,利用周期函数的定义证明即可.
(2)猜想是周期函数,利用周期函数的定义证明即可.
解答:
解:(1)证明:tan(x+
)=
=
. …(6分)
(2)猜想f(x)是以4a为周期的周期函数.
证明:因为f(x+2a)=f[(x+a)+a]=
=
=-
,
所以f(x+4a)=f[(x+2a)+2a]=-
=f(x),
所以f(x)是以4a为周期的周期函数. …(14分)
| π |
| 4 |
tanx+tan
| ||
1-tanx•tan
|
| 1+tanx |
| 1-tanx |
(2)猜想f(x)是以4a为周期的周期函数.
证明:因为f(x+2a)=f[(x+a)+a]=
| 1+f(x+a) |
| 1-f(x+a) |
1+
| ||
1-
|
| 1 |
| f(x) |
所以f(x+4a)=f[(x+2a)+2a]=-
| 1 |
| f(x+2a) |
所以f(x)是以4a为周期的周期函数. …(14分)
点评:本题考查三角函数的化简求值,周期的应用,基本知识的考查.

练习册系列答案
相关题目
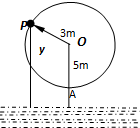 如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=
如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=