题目内容
甲、乙、丙三人同时各自解同一题,甲解答正确的概率为
,乙解答正确的概率为
,丙解答正确的概率为
,互相之间不受影响,求:
(1)三个人都解答正确的概率;
(2)只有一人解答正确的概率.
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
(1)三个人都解答正确的概率;
(2)只有一人解答正确的概率.
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)设A表示“甲解答正确”,B表示“乙解答正确”,C表示“丙解答正确”,则P(A)=
,P(B)=
,P(C)=
,由此利用相互独立事件乘法公式能求出三个人都解答正确的概率.
(2)只有一人解答正确的概率为P(A
)+P(
B
+
C),由此能求出结果.
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
(2)只有一人解答正确的概率为P(A
. |
| B |
. |
| C |
. |
| A |
. |
| C |
. |
| A |
. |
| B |
解答:
解:(1)设A表示“甲解答正确”,B表示“乙解答正确”,C表示“丙解答正确”,
则P(A)=
,P(B)=
,P(C)=
,
∴三个人都解答正确的概率:
P(ABC)=P(A)P(B)P(C)
=
×
×
=
.
(2)只有一人解答正确的概率:
P(A
)+P(
B
+
C)
=
×
×
+
×
×
+
×
×
=
.
则P(A)=
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
∴三个人都解答正确的概率:
P(ABC)=P(A)P(B)P(C)
=
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| 2 |
| 5 |
(2)只有一人解答正确的概率:
P(A
. |
| B |
. |
| C |
. |
| A |
. |
| C |
. |
| A |
. |
| B |
=
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 4 |
| 4 |
| 5 |
=
| 3 |
| 20 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意相互独立事件乘法公式的合理运用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目

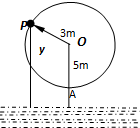 如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=
如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=