题目内容
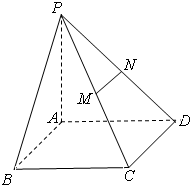 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,M、N分别是PC、PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,M、N分别是PC、PD的中点.(1)求证:MN∥平面PAB;
(2)若PA=2,AB=1,BC=
| 3 |
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)的证明可以利用线面平行的判定,
(2)先找到线PC与平面ABCD所成的角,后计算.
(2)先找到线PC与平面ABCD所成的角,后计算.
解答:
证:(1)∵M、N分别是PC、PD的中点,∵MN∥CD,
又AB∥CD,则MN∥AB,
而MN∥面PAB,AB?面PAB,
∴MN∥平面PAB平面; …..…(7分)
解:(2)由题意可知,AC是PC在平面ABCD上的射影,
则∠PCA是PC与平面ABCD所成的角,.…(10分)
因AC=
=2,又PA=2,
则△PAC是等腰直角三角形,∴∠PCA=45°,
即直线PC与平面ABCD所成的角为45°…(13分)
又AB∥CD,则MN∥AB,
而MN∥面PAB,AB?面PAB,
∴MN∥平面PAB平面; …..…(7分)
解:(2)由题意可知,AC是PC在平面ABCD上的射影,
则∠PCA是PC与平面ABCD所成的角,.…(10分)
因AC=
(
|
则△PAC是等腰直角三角形,∴∠PCA=45°,
即直线PC与平面ABCD所成的角为45°…(13分)
点评:本题考查线面平行的判定及线面角的计算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
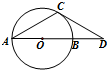 如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=
如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=