题目内容
已知定点F1(-
,0),F2(
,0),曲线C是使|RF1|+|RF2|为定值的点R的轨迹,曲线C过点T(0,1).
(1)求曲线C的方程;
(2)直线l过点F2,且与曲线C交于PQ,当△F1PQ的面积取得最大值时,求直线l的方程;
(3)设点P是曲线C上除长轴端点外的任一点,连接PF1、PF2,设∠F1PF2的角平分线PM交曲线C的长轴于点M(m,0),求m的取值范围.
| 3 |
| 3 |
(1)求曲线C的方程;
(2)直线l过点F2,且与曲线C交于PQ,当△F1PQ的面积取得最大值时,求直线l的方程;
(3)设点P是曲线C上除长轴端点外的任一点,连接PF1、PF2,设∠F1PF2的角平分线PM交曲线C的长轴于点M(m,0),求m的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出|RF1|+|RF2|=|TF1|+|TF2|≥2
,由此能求出曲线C的方程.
(2)设直线l为x=my+
,代入椭圆方程
+y2=1,得(4+m2)y2+2
my-1=0,由此利用韦达定理、点到直线距离公式,结合已知条件能求出直线l的方程.
(3)由题意知
=
,
=
,由此能求出m的取值范围.
| 3 |
(2)设直线l为x=my+
| 3 |
| x2 |
| 4 |
| 3 |
(3)由题意知
| ||||
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
|
解答:
解:(1)∵定点F1(-
,0),F2(
,0),
曲线C是使|RF1|+|RF2|为定值的点R的轨迹,
曲线C过点T(0,1).
∴|RF1|+|RF2|=|TF1|+|TF2|
=2
=4>|F1F2|=2
,(2分)
∴曲线C为以原点为中心,F1,F2为焦点的椭圆,
设其长半轴为a,短半轴为b,半焦距为c,
则2c=2
,∴a=2,c=
,b=1,
∴曲线C的方程为
+y2=1.(4分)
(2)设直线l为x=my+
,代入椭圆方程
+y2=1,
得(4+m2)y2+2
my-1=0,
△=12m2+16(m+m2)>0,
设P(x3,y3),得
,
∴|PQ|=
=
=
,
F1到直线l的距离d=
,
设t=
,则t≥1,
∴S△F1PQ=
|PQ|d=4
×
=
=
≤2.
当t2=3,即m2=2,m=±2时,面积最大,
∴△F1PQ的面积取得最大值时,
直线l的方程为:x+
y-
=0和x-
y-
=0.(9分)
(3)由题意可知:
=
,
=
,(10分)
设P(x0,y0)其中x02≠4,
将向量坐标代入并化简,得:
m(4x02-16)=3x02-12x0,(12分)
∵x02≠4,∴m=
x0,(13分)
∵x0∈(-2,2),∴m∈(-
,
).(14分)
| 3 |
| 3 |
曲线C是使|RF1|+|RF2|为定值的点R的轨迹,
曲线C过点T(0,1).
∴|RF1|+|RF2|=|TF1|+|TF2|
=2
(
|
| 3 |
∴曲线C为以原点为中心,F1,F2为焦点的椭圆,
设其长半轴为a,短半轴为b,半焦距为c,
则2c=2
| 3 |
| 3 |
∴曲线C的方程为
| x2 |
| 4 |
(2)设直线l为x=my+
| 3 |
| x2 |
| 4 |
得(4+m2)y2+2
| 3 |
△=12m2+16(m+m2)>0,
设P(x3,y3),得
|
∴|PQ|=
| (x3-x4)2+(y3-y4) |
=
| (1+m)2[(y3+y4)2-4y3y4] |
| 4(1+m2) |
| 4+m2 |
F1到直线l的距离d=
2
| ||
|
设t=
| 1+m2 |
∴S△F1PQ=
| 1 |
| 2 |
| 3 |
| ||
| 4+m2 |
4
| ||
| t2+3 |
4
| ||
t+
|
当t2=3,即m2=2,m=±2时,面积最大,
∴△F1PQ的面积取得最大值时,
直线l的方程为:x+
| 2 |
| 3 |
| 2 |
| 3 |
(3)由题意可知:
| ||||
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
|
设P(x0,y0)其中x02≠4,
将向量坐标代入并化简,得:
m(4x02-16)=3x02-12x0,(12分)
∵x02≠4,∴m=
| 3 |
| 4 |
∵x0∈(-2,2),∴m∈(-
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查曲线方程的求法,考查三角形面积最大时直线方程的求法,考查实数的取值范围的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=lg
的图象( )
| 1+sinx |
| cosx |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
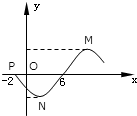 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象的一部分如图,已知函数与x轴交于点P(-2,0)和(6,0),点M,N分别是最高点和最低点,且∠MPN=
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象的一部分如图,已知函数与x轴交于点P(-2,0)和(6,0),点M,N分别是最高点和最低点,且∠MPN= 2013年某市某区高考文科数学成绩抽样统计如下表:
2013年某市某区高考文科数学成绩抽样统计如下表: