题目内容
 2013年某市某区高考文科数学成绩抽样统计如下表:
2013年某市某区高考文科数学成绩抽样统计如下表:| 分组 | 频数 | 频率 | 频率/组距 |
| [0,30) | 6 | 0.006 | 0.0002 |
| [30,60) | 82 | 0.082 | 0.0027 |
| [60,90) | 256 | 0.256 | 0.0085 |
| [90,120) | m | n | 0.0145 |
| [120,150] | 220 | N | 0.0073 |
| 合计 | M | 1 |
(Ⅱ)若2013年北京市高考文科考生共有20000人,试估计全市文科数学成绩在90分及90分以上的人数;
(Ⅲ)香港某大学对内地进行自主招生,在参加面试的学生中,有7名学生数学成绩在140分以上,其中男生有4名,要从7名学生中录取2名学生,求其中恰有1名女生被录取的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:计算题,作图题,概率与统计
分析:(I)根据频率=
求频率、频数及样本容量,根据各小矩形的高作频率分布直方图;
(II)利用样本来估计总体的思想,根据样本中的比例估计总体中90分及90分以上的人数;
(III)写出所有基本事件,从中找出恰有1名女生的基本事件,利用基本事件个数比求概率.
| 频数 |
| 样本容量 |
(II)利用样本来估计总体的思想,根据样本中的比例估计总体中90分及90分以上的人数;
(III)写出所有基本事件,从中找出恰有1名女生的基本事件,利用基本事件个数比求概率.
解答:
解:(Ⅰ)由统计表知:M=
=1000,
m=1000-6-82-256-220=436,
n=
=0.436,N=
=0.220.
频率分布直方图如图:
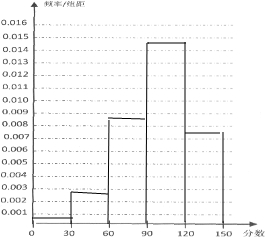
(Ⅱ)设全市文科数学成绩在90及90分以上的人数为x,
则
=
,x=13120;
(Ⅲ)设4名男生分别表示为A1、A2、A3、A4,
3名女生分别表示为B1、B2、B3,
则从7名学生中录取2名学生的基本事件有:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A1,B3),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A2,B3),(A3,A4),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),
(B1,B2),(B1,B3),(B2,B3),共21种
设“选2人恰有1名女生”为事件A,有:
(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),
共12种,
∴P(A)=
=
.
故7人中录取2人恰有1人为女生的概率为:
.
| 6 |
| 0.006 |
m=1000-6-82-256-220=436,
n=
| 436 |
| 1000 |
| 220 |
| 1000 |
频率分布直方图如图:

(Ⅱ)设全市文科数学成绩在90及90分以上的人数为x,
则
| 1000 |
| 20000 |
| 656 |
| x |
(Ⅲ)设4名男生分别表示为A1、A2、A3、A4,
3名女生分别表示为B1、B2、B3,
则从7名学生中录取2名学生的基本事件有:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A1,B3),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A2,B3),(A3,A4),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),
(B1,B2),(B1,B3),(B2,B3),共21种
设“选2人恰有1名女生”为事件A,有:
(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),
共12种,
∴P(A)=
| 12 |
| 21 |
| 4 |
| 7 |
故7人中录取2人恰有1人为女生的概率为:
| 4 |
| 7 |
点评:本题考查了频率分布直方图的作法及利用频率分布直方图求频数,考查了古典概型的概率计算,利用列举法写出所有基本事件是古典概型求概率的常用方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目