题目内容
过定点A(3,4)任作互相垂直的两条线l1与l2,且l1与x轴交于M点,l2与y轴交于N点,求线段MN中点P的轨迹方程.
考点:与直线有关的动点轨迹方程
专题:直线与圆
分析:通过当l1不平行于坐标轴时,设l1:y-4=k(x-3),l2:y-4=-
(x-3)求出M(3-
,0),求出N(0,4+
)
设MN的中点P(x,y),消去k得轨迹方程,当l1平行于坐标轴时,判断是否满足方程即可.
| 1 |
| k |
| 4 |
| k |
| 3 |
| k |
设MN的中点P(x,y),消去k得轨迹方程,当l1平行于坐标轴时,判断是否满足方程即可.
解答:
(本小题满分12分)
解:当l1不平行于坐标轴时,设l1:y-4=k(x-3)…①
则k≠0,∴l2:y-4=-
(x-3)…②
在①中令y=0得,M(3-
,0),在②中令x=0得,N(0,4+
)
设MN的中点P(x,y),则
消去k得,6x+8y-25=0,
当l1平行于坐标轴时,MN的中点为(
,2)也满足此方程.
∴P点的轨迹方程为6x+8y-25=0.
解:当l1不平行于坐标轴时,设l1:y-4=k(x-3)…①
则k≠0,∴l2:y-4=-
| 1 |
| k |
在①中令y=0得,M(3-
| 4 |
| k |
| 3 |
| k |
设MN的中点P(x,y),则
|
当l1平行于坐标轴时,MN的中点为(
| 3 |
| 2 |
∴P点的轨迹方程为6x+8y-25=0.
点评:本题考查轨迹方程的求法,注意直线的斜率是否存在是解题的易错点.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知两条相交直线a、b,a∥平面α,则b与平面α的位置关系( )
| A、b∥α |
| B、b与α相交 |
| C、b?α |
| D、b∥α或b与α相交 |
设M(x,y)是区域
内的动点,且不等式x+2y≤14恒成立,则实数a的取值范围是( )
|
| A、[8,10] |
| B、[8,9] |
| C、[6,9] |
| D、[6,10] |
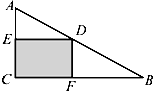 在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.
在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.