题目内容
已知等比数列{an}满足a1+a2=3，a2+a3=6，则a5= ．
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据等比数列的条件，建立方程组求出等比数列的首项和公比即可得到结论．
解答：
解：在等比数列中，a1+a2=3，a2+a3=6，
则q=
=
=2，
又a1+a2=a1+2a1=3a1=3，
解得a1=1，
∴a5=24=16，
故答案为：16
则q=
| a2+a3 |
| a1+a2 |
| 6 |
| 3 |
又a1+a2=a1+2a1=3a1=3，
解得a1=1，
∴a5=24=16，
故答案为：16
点评：本题主要考查等比数列的通项公式的应用，利用条件建立方程组是解决本题的关键．
练习册系列答案
小学教材全测系列答案
相关题目
执行如图所示的程序框图，若输入n的值为7，则输出s的值是（ ）
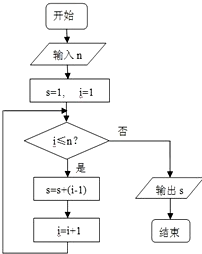
| A、10 | B、16 | C、22 | D、17 |
已知实数x∈[1，10]，执行如图所示的流程图，则输出的x不小于63的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知某山区小学有100名四年级学生，将全体四年级学生随机按00～99编号，并且按编号顺序平均分成10组．现要从中抽取10名学生，各组内抽取的编号按依次增加10进行系统抽样．