题目内容
7.已知角φ的终边经过点P(1,1),函数f(x)=sin(ωx+φ)(ω>0)图象的相邻两条对称轴之间的距离等于$\frac{π}{3}$,则$f({\frac{π}{6}})$=( )| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由题意可得φ可取$\frac{π}{4}$,再由函数图象和周期公式可得ω=3,代值计算可得.
解答 解:∵角φ的终边经过点P(1,1),∴φ可取$\frac{π}{4}$,
又∵函数f(x)=sin(ωx+φ)图象的相邻两条对称轴之间的距离等于$\frac{π}{3}$,
∴函数f(x)的周期为$\frac{2π}{3}$,故$\frac{2π}{ω}$=$\frac{2π}{3}$,解得ω=3,
∴$f({\frac{π}{6}})$=sin(3×$\frac{π}{6}$+$\frac{π}{4}$)=sin$\frac{3π}{4}$=$\frac{\sqrt{2}}{2}$,
故选:B.
点评 本题考查正弦函数的图象和性质,涉及三角函数的周期公式,属基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
20.今有点A(-4,3)在双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)上,过点A的直线l与双曲线相切,且与双曲线两渐近线围成的三角形面积为2$\sqrt{3}$,则直线l的方程为( )
| A. | x+y+1=0 | B. | 2x+y+5=0 | C. | 2x+3y+1=0 | D. | x+3y-5=0 |
18.若函数$f(x)={log_{\frac{1}{3}}}x+\frac{1}{x}+a$的零点在区间(1,+∞)上,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (-∞,-1) | C. | (-1,+∞) | D. | (0,+∞) |
12.已知$tan({x+\frac{π}{4}})=2$,则sin2x=( )
| A. | $-\frac{3}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{3}{5}$ | D. | 1 |
19.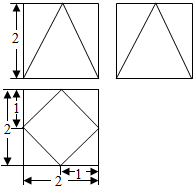 一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
 一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )| A. | 4 | B. | $\frac{20}{3}$ | C. | $\frac{4}{3}$(3+$\sqrt{2}$) | D. | $\frac{16}{3}$ |
16.若在平面直角坐标中,方程x2+2xsinxy+1=0所表示的图形为( )
| A. | 直线 | B. | 抛物线 | C. | 一个点 | D. | 以上都不对 |
15.一个与正整数n有关的命题,当n=2时命题成立,且由n=k时命题成立可以推得n=k+2时命题也成立,则( )
| A. | 该命题对于n>2的自然数n都成立 | B. | 该命题对于所有的正偶数都成立 | ||
| C. | 该命题何时成立与k取值无关 | D. | 以上答案都不对 |