题目内容
15.在棱长为2的正四面体P-ABC中,M,N分别为PA,BC的中点,点D是线段PN上一点,且PD=2DN,则三棱锥P-MBD的体积为$\frac{\sqrt{2}}{9}$.分析 由题意画出图形,由已知条件求出D到平面PAB的距离,把三棱锥P-MBD的体积转化为三棱锥D-PBM的体积求解.
解答 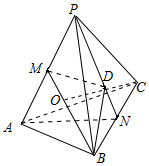 解:如图:
解:如图:
∵P-ABC为正四面体,且棱长为2,
∴C在底面PAB的射影为底面三角形PAB的外心O,也是重心,
则BM=$\sqrt{3}$,BO=$\frac{2\sqrt{3}}{3}$,
∴$CO=\sqrt{{2}^{2}-(\frac{2\sqrt{3}}{3})^{2}}=\frac{2\sqrt{6}}{3}$,
又N为BC的中点,PD=2DN,
D到面PAB的距离为$\frac{2}{3}×\frac{1}{2}CO=\frac{1}{3}×\frac{2\sqrt{6}}{3}=\frac{2\sqrt{6}}{9}$,
而${S}_{△PBM}=\frac{1}{2}×1×\sqrt{3}=\frac{\sqrt{3}}{2}$,
∴${V}_{P-MBD}={V}_{D-PBM}=\frac{1}{3}×\frac{\sqrt{3}}{2}×\frac{2\sqrt{6}}{9}=\frac{\sqrt{2}}{9}$.
故答案为:$\frac{\sqrt{2}}{9}$.
点评 本题考查棱柱、棱锥及棱台的体积,考查学生的空间想象能力和思维能力,训练了等积法在求多面体体积中的应用,是中档题.

练习册系列答案
相关题目
9.复数$\frac{1-{i}^{3}}{1+3i}$=( )
| A. | -$\frac{2}{5}$+$\frac{1}{5}$i | B. | -$\frac{2}{5}$-$\frac{1}{5}$i | C. | $\frac{2}{5}$+$\frac{1}{5}$i | D. | $\frac{2}{5}$-$\frac{1}{5}$i |
10.近日,济南楼市迎来去库存一系列新政,其中房产税收中的契税和营业税双双下调,对住房市场持续增长和去库存产生积极影响.某房地产公司从两种户型中各拿出9套进行促销活动,其中A户型每套面积100平方米,均价1.1万元/平方米,B户型每套面积80平方米,均价1.2万元/平方米.下表是这18套住宅平方米的销售价格:(单位:万元/平方米):
(I)求a,b的值;
(II)张先生想为自己和父母买两套售价小于100万元的房子,求至少有一套面积为100平方米的概率.
| 房号/户型 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A户型 | 0.98 | 0.99 | 1.06 | 1.17 | 1.10 | 1.21 | a | 1.09 | 1.14 |
| B户型 | 1.08 | 1.11 | 1.12 | b | 1.26 | 1.27 | 1.26 | 1.25 | 1.28 |
(II)张先生想为自己和父母买两套售价小于100万元的房子,求至少有一套面积为100平方米的概率.
7.已知角φ的终边经过点P(1,1),函数f(x)=sin(ωx+φ)(ω>0)图象的相邻两条对称轴之间的距离等于$\frac{π}{3}$,则$f({\frac{π}{6}})$=( )
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
4.已知f(x)为偶函数,当x≥0时,f(x)=m(|x-2|+|x-4|),(m>0),若函数y=f[f(x)]-4m恰有4个零点,则实数m的取值范围( )
| A. | $({0,\frac{1}{6}})$ | B. | $({0,\frac{1}{6}})∪({\frac{5}{6},\frac{5}{2}})$ | C. | $({0,\frac{1}{4}})∪({\frac{5}{4},\frac{5}{2}})$ | D. | $({0,\frac{1}{4}})$ |
5.将函数f(x)=-cos2x的图象向右平移$\frac{π}{4}$个单位后得到函数g(x),则g(x)具有性质( )
| A. | 最大值为1,图象关于直线x=$\frac{π}{2}$对称 | B. | 在(0,$\frac{π}{4}$)上单调递减,为奇函数 | ||
| C. | 在(-$\frac{3π}{8}$,$\frac{π}{8}$)上单调递增,为偶函数 | D. | 周期为π,图象关于点($\frac{3π}{8}$,0)对称 |