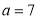题目内容
20.今有点A(-4,3)在双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)上,过点A的直线l与双曲线相切,且与双曲线两渐近线围成的三角形面积为2$\sqrt{3}$,则直线l的方程为( )| A. | x+y+1=0 | B. | 2x+y+5=0 | C. | 2x+3y+1=0 | D. | x+3y-5=0 |
分析 对双曲线的方程两边对x求导,可得A点处切线的斜率和切线方程,联立渐近线方程,可得交点M,N的坐标,求得点O到切线的距离,以及两点MN的距离,运用三角形的面积公式,化简整理,结合点A在双曲线上,可得ab=2$\sqrt{3}$,
解方程可得a,b,进而得到所求直线l的方程.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1,对x求导,可得
$\frac{2x}{{a}^{2}}$-$\frac{2yy′}{{b}^{2}}$=0,
点A的直线l的斜率为-$\frac{4{b}^{2}}{3{a}^{2}}$,
可得切线的方程为y=-$\frac{4{b}^{2}}{3{a}^{2}}$x-$\frac{{b}^{2}}{3}$,
双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{a}$x,
联立切线的方程可得,交点为M(-$\frac{{a}^{2}b}{3a+4b}$,-$\frac{a{b}^{2}}{3a+4b}$),N($\frac{{a}^{2}b}{3a-4b}$,-$\frac{a{b}^{2}}{3a-4b}$),
可得|MN|=$\frac{2ab\sqrt{9{a}^{4}+16{b}^{4}}}{|9{a}^{2}-16{b}^{2}|}$,
点O到切线的距离为d=$\frac{{a}^{2}{b}^{2}}{\sqrt{9{a}^{4}+16{b}^{4}}}$,
由题意可得围成三角形的面积为$\frac{1}{2}$•$\frac{{a}^{2}{b}^{2}}{\sqrt{9{a}^{4}+16{b}^{4}}}$•$\frac{2ab\sqrt{9{a}^{4}+16{b}^{4}}}{|9{a}^{2}-16{b}^{2}|}$=2$\sqrt{3}$,
即为$\frac{{a}^{3}{b}^{3}}{|9{a}^{2}-16{b}^{2}|}$=2$\sqrt{3}$,
由点A(-4,3)在双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1上,可得$\frac{16}{{a}^{2}}$-$\frac{9}{{b}^{2}}$=1,
即为9a2-16b2=-a2b2,
即有ab=2$\sqrt{3}$,
解得a=2,b=$\sqrt{3}$,
则直线l的方程为y=-x-1,
即为x+y+1=0.
故选:A.
点评 本题考查双曲线的方程的运用,直线与双曲线相切,联立直线方程求交点,以及点到直线的距离公式,考查运算化简能力,属于中档题.

| A. | -$\frac{2}{5}$+$\frac{1}{5}$i | B. | -$\frac{2}{5}$-$\frac{1}{5}$i | C. | $\frac{2}{5}$+$\frac{1}{5}$i | D. | $\frac{2}{5}$-$\frac{1}{5}$i |
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
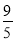 ,则( )
,则( ) 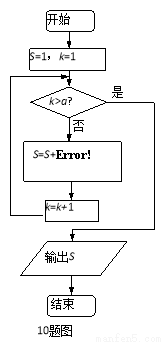
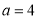 B.
B.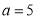 C.
C.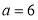 D.
D.