题目内容
19．
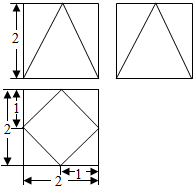一个正方体截去四个角得到一个多面体，其三视图如图所示，则该多面体的体积为（ ）| A． | 4 | B． | $\frac{20}{3}$ | C． | $\frac{4}{3}$（3+$\sqrt{2}$） | D． | $\frac{16}{3}$ |
分析 由已知中的三视图可得该几何体是一个正方体截去四个角得到一个多面体，进而可得答案．
解答 解：由已知中的三视图可得该几何体是一个正方体截去四个角得到一个多面体，
正方体的体积为：8，
每个角的体积均为：$\frac{1}{3}$×（$\frac{1}{2}$×1×1）×2=$\frac{1}{3}$，
故组合体的体积V=8-4×$\frac{1}{3}$=$\frac{20}{3}$，
故选：B．
点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．
练习册系列答案
口算题天天练系列答案
相关题目
10．近日，济南楼市迎来去库存一系列新政，其中房产税收中的契税和营业税双双下调，对住房市场持续增长和去库存产生积极影响．某房地产公司从两种户型中各拿出9套进行促销活动，其中A户型每套面积100平方米，均价1.1万元/平方米，B户型每套面积80平方米，均价1.2万元/平方米．下表是这18套住宅平方米的销售价格：（单位：万元/平方米）：
（I）求a，b的值；
（II）张先生想为自己和父母买两套售价小于100万元的房子，求至少有一套面积为100平方米的概率．
| 房号/户型 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A户型 | 0.98 | 0.99 | 1.06 | 1.17 | 1.10 | 1.21 | a | 1.09 | 1.14 |
| B户型 | 1.08 | 1.11 | 1.12 | b | 1.26 | 1.27 | 1.26 | 1.25 | 1.28 |
（II）张先生想为自己和父母买两套售价小于100万元的房子，求至少有一套面积为100平方米的概率．
7．已知角φ的终边经过点P（1，1），函数f（x）=sin（ωx+φ）（ω＞0）图象的相邻两条对称轴之间的距离等于$\frac{π}{3}$，则$f（{\frac{π}{6}}）$=（ ）
| A． | $-\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
14．已知函数f（x）=sinπx和函数g（x）=cosπx在区间[-1，2]上的图象交于 A、B、C三点，则△ABC的面积是（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{3\sqrt{2}}}{4}$ | C． | $\sqrt{2}$ | D． | $\frac{{5\sqrt{2}}}{4}$ |
4．已知f（x）为偶函数，当x≥0时，f（x）=m（|x-2|+|x-4|），（m＞0），若函数y=f[f（x）]-4m恰有4个零点，则实数m的取值范围（ ）
| A． | $（{0，\frac{1}{6}}）$ | B． | $（{0，\frac{1}{6}}）∪（{\frac{5}{6}，\frac{5}{2}}）$ | C． | $（{0，\frac{1}{4}}）∪（{\frac{5}{4}，\frac{5}{2}}）$ | D． | $（{0，\frac{1}{4}}）$ |
8．为了了解某天甲乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14和5件，测量产品中的微量元素x，y的含量（单位：毫克）．当产品中的微量元素x，y满足x≥175，且y≥75时，该产品为优等品．已知甲厂该天生产的产品共有98件，如表是乙厂的5件产品的测量数据：
（I）求乙厂该天生产的产品数量；
（Ⅱ）从乙厂抽出取上述5件产品中，随机抽取2件，求抽取的2件产品中优等品至少有1件的概率．
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
（Ⅱ）从乙厂抽出取上述5件产品中，随机抽取2件，求抽取的2件产品中优等品至少有1件的概率．
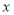的一元二次方程
．
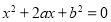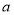是从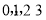
四个数中任取的一个数，
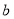是从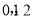
三个数中任取的一个数，求上述方程有实根的概率；
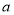是从区间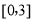
任取的一个数，
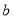是从区间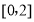
任取的一个数，求上述方程有实根的概率．