题目内容
已知函数f（x）=x2-2ax+6在区间（-∞，3）是减函数，则（ ）
| A、a≥3 | B、a＞0 |
| C、a≤3 | D、a＜3 |
考点：二次函数的性质
专题：函数的性质及应用
分析：求出函数的对称轴，然后求f（x）在区间（-∞，3）是减函数，求出a的取值范围．
解答：
解：函数f（x）=x2-2ax+6的开口向上，对称轴为x=a，
函数f（x）=x2-2ax+6在区间（-∞，3）是减函数，
∴a≥3．
故选：A．
函数f（x）=x2-2ax+6在区间（-∞，3）是减函数，
∴a≥3．
故选：A．
点评：本题主要考查了函数单调性的应用，解题的关键是比较区间端点与二次函数的对称轴的大小．
练习册系列答案
相关题目
如图所示的三视图的几何体的体积为（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
确定结论“X与Y有关系”的可信度为99.5%时，则随即变量k2的观测值k必须（ ）
| A、小于7.879 |
| B、大于10.828 |
| C、小于6.635 |
| D、大于2.706 |
如图，在平行六面体ABCD-A1B1C1D1中，M为A1C1，B1D1的交点，N是棱BC的中点，若| AB |
| a |
| AD |
| b |
| AA |
| c |
| MN |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
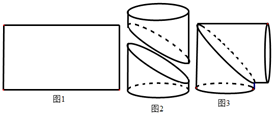工人师傅在如图1的一块矩形铁皮上画一条曲线，沿曲线剪开，将所得到的两部分卷成圆柱状，如图2，然后将其对接，可做成一个直角的“拐脖”，如图3．工人师傅所画的曲线是（ ）| A、一段圆弧 |
| B、一段抛物线 |
| C、一段双曲线 |
| D、一段正弦曲线 |
如果椭圆
+
=1上一点p到焦点F1的距离等于3，那么点p到另一个焦点F2的距离是（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| A、4 | B、3 | C、2 | D、1 |
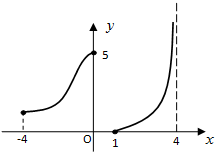如图所示是函数y=f（x）的图象，图中曲线与直线无限接近但是永不相交，则以下描述正确的是（ ）| A、函数f（x）的定义域为[-4，4） |
| B、函数f（x）的值域为[0，5] |
| C、此函数在定义域中不单调 |
| D、对于任意的y∈[0，+∞），都有唯一的自变量x与之对应 |