题目内容
3.已知四边形OADB是以向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$为边的平行四边形,点C为对角线AB,OD的交点,$\overrightarrow{BM}=\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{CN}=\frac{1}{3}\overrightarrow{CD}$(1)试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OM},\overrightarrow{ON},\overrightarrow{MN}$;
(2)若OA=2,OB=6,MN=1,求平行四边形OADB的面积.
分析 (1)运用向量的加减运算和平面向量的基本定理,化简整理即可得到所求;
(2)由题意可得|$\overrightarrow{MN}$|=1=|$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{6}$$\overrightarrow{b}$|,两边平方,结合向量的数量积的定义,再由平行四边形的面积公式计算即可得到所求值.
解答 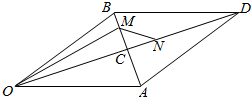 解:(1)$\overrightarrow{BM}=\frac{1}{3}\overrightarrow{BC}$,可得$\overrightarrow{OM}$-$\overrightarrow{OB}$=$\frac{1}{3}$($\overrightarrow{OC}$-$\overrightarrow{OB}$)
解:(1)$\overrightarrow{BM}=\frac{1}{3}\overrightarrow{BC}$,可得$\overrightarrow{OM}$-$\overrightarrow{OB}$=$\frac{1}{3}$($\overrightarrow{OC}$-$\overrightarrow{OB}$)
即有$\overrightarrow{OM}$=$\frac{1}{3}$$\overrightarrow{OC}$+$\frac{2}{3}$$\overrightarrow{OB}$=$\frac{1}{6}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)+$\frac{2}{3}$$\overrightarrow{OB}$=$\frac{1}{6}$$\overrightarrow{OA}$+$\frac{5}{6}$$\overrightarrow{OB}$
=$\frac{1}{6}$$\overrightarrow{a}$+$\frac{5}{6}$$\overrightarrow{b}$;
由$\overrightarrow{CN}$=$\frac{1}{3}$$\overrightarrow{CD}$,可得$\overrightarrow{ON}$-$\overrightarrow{OC}$=$\frac{1}{3}$($\overrightarrow{OD}$-$\overrightarrow{OC}$),
即有$\overrightarrow{ON}$=$\frac{1}{3}$$\overrightarrow{OD}$+$\frac{2}{3}$$\overrightarrow{OC}$=$\frac{1}{3}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)+$\frac{1}{3}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)
=$\frac{2}{3}$($\overrightarrow{a}$+$\overrightarrow{b}$);
$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$=$\frac{2}{3}$($\overrightarrow{a}$+$\overrightarrow{b}$)-$\frac{1}{6}$$\overrightarrow{a}$-$\frac{5}{6}$$\overrightarrow{b}$=$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{6}$$\overrightarrow{b}$;
(2)由题意可得|$\overrightarrow{MN}$|=1=|$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{6}$$\overrightarrow{b}$|,
即有1=$\frac{1}{4}$$\overrightarrow{a}$2-$\frac{1}{6}$$\overrightarrow{a}$•$\overrightarrow{b}$+$\frac{1}{36}$$\overrightarrow{b}$2=$\frac{1}{4}$×4-$\frac{1}{6}$×2×6cos<$\overrightarrow{a}$,$\overrightarrow{b}$>+$\frac{1}{36}$×36,
可得cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,
即有sin<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\sqrt{1-\frac{1}{4}}$=$\frac{\sqrt{3}}{2}$,
则平行四边形OADB的面积为|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•sin<$\overrightarrow{a}$,$\overrightarrow{b}$>=2×6×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$.
点评 本题考查向量的加减和平面向量的基本定理的运用,考查向量的数量积的定义、性质,考查运算能力,属于中档题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案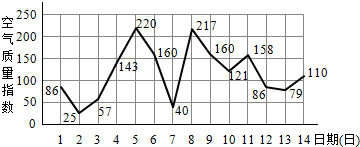 如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).(Ⅰ)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(Ⅱ)求此人到达当日空气质量优良的概率;
(Ⅲ)求此人出差期间(两天)空气质量至少有一天为中度或重度污染的概率.
| 空气质量指数 | 污染程度 |
| 小于100 | 优良 |
| 大于100且小于150 | 轻度 |
| 大于150且小于200 | 中度 |
| 大于200且小于300 | 重度 |
| 大于300且小于500 | 严重 |
| 大于500 | 爆表 |
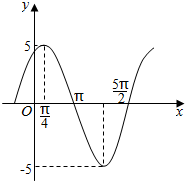 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).