题目内容
11.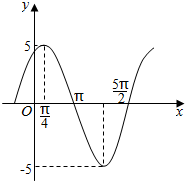 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).
分析 根据条件下求出A,ω和φ的值即可求函数的表达式
解答 解:由图象知A=5,且$\frac{1}{2}$T=$\frac{5π}{2}$-π=$\frac{3π}{2}$,
即T=3π.
即$\frac{2π}{ω}$=3π得ω=$\frac{2}{3}$,
则y=5sin($\frac{2}{3}$x+φ),
即当x=$\frac{π}{4}$时,y=5sin($\frac{2}{3}$×$\frac{π}{4}$+φ)=5,
即sin($\frac{π}{6}$+φ)=1,
即$\frac{π}{6}$+φ=2kπ+$\frac{π}{2}$,即φ=2kπ+$\frac{π}{3}$,
∵|φ|<π,
∴当k=0时,φ=$\frac{π}{3}$,
即y=5sin($\frac{2}{3}$x+$\frac{π}{3}$),
故答案为:5sin($\frac{2}{3}$x+$\frac{π}{3}$)
点评 本题主要考查三角函数解析式的求解,利用图象求出函数的解析式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若反比例函数f(x)=$\frac{k}{x}$的图象在第一象限内单调递减,则k的取值范围( )
| A. | k≥0 | B. | k≤0 | C. | k>0 | D. | k<0 |
2.下列大小关系正确的是( )
| A. | ${3^{\frac{1}{3}}}>{4^{\frac{1}{3}}}$ | B. | 0.30.4>0.30.3 | C. | log76<log67 | D. | sin3>sin2 |
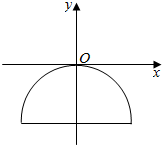 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度为16m,跨度为40m.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度为16m,跨度为40m.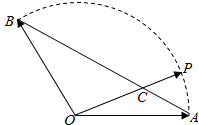 如图,已知不共线的两个单位向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为120°,点C在线段AB上,设向量$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).
如图,已知不共线的两个单位向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为120°,点C在线段AB上,设向量$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).