题目内容
12.已知a>0,b∈R,函数f(x)=4ax2-2bx-a+b的定义域为[0,1].(1)当a=1时,函数f(x)在定义域内有两个不同的零点,求b的取值范围;
(2)设f(x)的最大值和最小值分别为M和m,求证:M+m>0.
分析 (1)由题意可得f(0)≥0,f(1)≥0,△>0,0<$\frac{b}{4}$<1,解不等式即可得到所求范围;
(2)求出对称轴,讨论对称轴和区间[0,1]的关系,可得最值,即可证明M+m>0.
解答 解:(1)由题意可得f(x)=4x2-2bx-1+b在[0,1]内有两个不同的零点,
即有$\left\{\begin{array}{l}{f(0)=b-1≥0}\\{f(1)=3-b≥0}\\{△=4{b}^{2}-16(b-1)>0}\\{0<\frac{b}{4}<1}\end{array}\right.$即为$\left\{\begin{array}{l}{b≥1}\\{b≤3}\\{b≠2}\\{0<b<4}\end{array}\right.$,
解得1≤b<2或2<b≤3;
(2)证明:f(x)的对称轴为x=$\frac{b}{4a}$,
当$\frac{b}{4a}$>1时,区间[0,1]为减区间,可得M=f(0)=b-a,
m=f(1)=3a-b,则M+m=2a>0;
当$\frac{b}{4a}$<0时,区间[0,1]为增区间,可得m=f(0)=b-a,
M=f(1)=3a-b,则M+m=2a>0;
当0≤$\frac{b}{4a}$≤1时,区间[0,$\frac{b}{4a}$]为减区间,[$\frac{b}{4a}$,1]为增区间,
可得m=f($\frac{b}{4a}$)=$\frac{4ab-4{a}^{2}-{b}^{2}}{4a}$,
若f(0)≤f(1),即b≤2a,可得M=f(1)=3a-b,
M+m=$\frac{8{a}^{2}-{b}^{2}}{4a}$≥$\frac{8{a}^{2}-4{a}^{2}}{4a}$=a>0;
若f(0)>f(1),即2a<b≤4a,可得M=f(0)=b-a,
M+m=$\frac{8ab-8{a}^{2}-{b}^{2}}{4a}$=$\frac{-(b-4a)^{2}+8{a}^{2}}{4a}$,
由于2a<b≤4a,可得M+m∈(a,2a],即为M+m>0.
综上可得M+m>0恒成立.
点评 本题考查函数的零点问题的解法,注意运用二次函数的图象,考查函数的最值的求法,注意讨论对称轴和区间的关系,考查运算能力,属于中档题.

| A. | ${3^{\frac{1}{3}}}>{4^{\frac{1}{3}}}$ | B. | 0.30.4>0.30.3 | C. | log76<log67 | D. | sin3>sin2 |
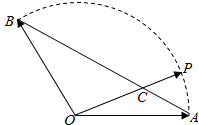 如图,已知不共线的两个单位向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为120°,点C在线段AB上,设向量$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).
如图,已知不共线的两个单位向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为120°,点C在线段AB上,设向量$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).