题目内容
14.经市场调查,某种商品在80天内的日销售量Q(千克)和售价P(元/千克)均为时间t(天)的函数,日销售量Q与时间t的关系如图1所示,售价P与时间t的关系如图2所示.(1)写出图1表示的日销售量Q与时间t的函数关系式Q=g(t);写出图(2)表示的售价P与时间t的函数关系式P=f(t);
(2)求日销售额y(元)与时间t的函数关系式,并求出日销售额最高的是哪一天?最高的销售额是多少?(注:日销售额=日销售量×售价).
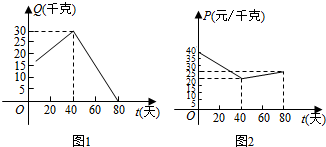
分析 (1)可看出图1和图2都是两条线段构成的图象,每段线段的端点坐标可以确定,从而可根据点斜式方程写出每条线段对应的方程,这样即可得出$g(t)=\left\{\begin{array}{l}{\frac{3}{8}t+15}&{0≤t<40}\\{-\frac{3}{4}t+60}&{40≤t≤80}\end{array}\right.$,$f(t)=\left\{\begin{array}{l}{-\frac{1}{2}t+40}&{0≤t<40}\\{-\frac{3}{4}t+60}&{40≤t≤80}\end{array}\right.$;
(2)根据题意知y=g(t)f(t),g(t)与f(t)相乘会得到每段函数为二次函数的分段函数,然后配方即可求出每段上y的最大值,比较这两个最大值便可得出y的最大值,以及对应的t值,即得出日销售额最高的是哪一天,以及最高的销售额是多少.
解答 解:(1)根据图1看出,图象过点(0,15),(40,30),(80,0);
∴两条直线的斜率分别为$\frac{30-15}{40-0}=\frac{3}{8}$,$\frac{30-0}{40-80}=-\frac{3}{4}$;
∴$g(t)=\left\{\begin{array}{l}{\frac{3}{8}t+15}&{0≤t<40}\\{-\frac{3}{4}t+60}&{40≤t≤80}\end{array}\right.$;
根据图2看出,图象过点(0,40),(40,20),(80,25);
∴两直线的斜率分别为$\frac{40-20}{0-40}=-\frac{1}{2},\frac{25-20}{80-40}=\frac{1}{8}$;
∴$f(t)=\left\{\begin{array}{l}{-\frac{1}{2}t+40}&{0≤t<40}\\{\frac{1}{8}t+15}&{40≤t≤80}\end{array}\right.$;
(2)y=g(t)f(t)=$\left\{\begin{array}{l}{-\frac{3}{16}(t-20)^{2}+675}&{0≤t<40}\\{-\frac{3}{32}(t+20)^{2}+\frac{1875}{2}}&{40≤t≤80}\end{array}\right.$;
∴①0≤t<40时,t=20时,y取到最大值675;
②40≤t≤80时,t=40时,y取到最大值600;
∴日销售额最高的是第20天,最高的销售额是675元.
点评 考查由两点坐标求过这两点直线斜率的计算公式,直线的点斜式方程,分段函数的概念及表示形式,以及配方法求二次函数的最值.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | (-∞,-4) | B. | (4,+∞) | C. | (-∞,-4$\sqrt{2}$) | D. | (4$\sqrt{2}$,+∞) |
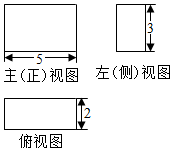
| A. | 19π | B. | 30π | C. | 38π | D. | $\frac{{19\sqrt{38}}}{3}π$ |
| A. | ${3^{\frac{1}{3}}}>{4^{\frac{1}{3}}}$ | B. | 0.30.4>0.30.3 | C. | log76<log67 | D. | sin3>sin2 |
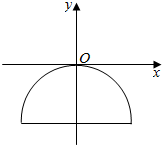 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度为16m,跨度为40m.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度为16m,跨度为40m.