题目内容
3.已知集合A={x|(m-1)x2+3x-2=0}.(1)若集合A为两个元素的集合,试求实数m的范围;
(2)是否存在这样的实数m,使得集合A有仅有两个子集?若存在,求出所有的m的值组成的集合M;若不存在,请说明理由.
分析 (1)若集合A为两个元素的集合,则关于x的方程有实数解,则m-1≠0,由此根据判别式能求出实数m的取值范围;
(2)若A恰有两个子集,则A为单元素集,即关于x的方程(m-1)x2+3x-2=0恰有一个实数解,求出实数m的取值范围即可得答案.
解答 解:(1)若集合A为两个元素的集合,则关于x的方程(m-1)x2+3x-2=0有实数解,则m-1≠0,
且△=9+8(m-1)>0,∴$m>-\frac{1}{8}$;
(2)集合A且仅有两个子集,
∴关于x的方程恰有一个实数解,
讨论:①当m=1时,x=$\frac{2}{3}$,满足题意;
②当m≠1时,△=8m+1=0,∴m=-$\frac{1}{8}$.
综上所述,m=1或m=-$\frac{1}{8}$.
∴M的集合为{-$\frac{1}{8}$,1}.
点评 本题考查实数m的取值范围的求法,解题时要认真审题,注意分析法、讨论法的合理运用,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知函数$f(x)=1+x-\frac{x^2}{2}+\frac{x^3}{3}-…+\frac{{{x^{2017}}}}{2017}$,设F(x)=f(x+4),且F(x)的零点均在区间(a,b)内,其中a,b∈Z,a<b,则F(x)>0的最小整数解为( )
| A. | -1 | B. | 0 | C. | -5 | D. | -4 |
12.要得到函数$y=sin({3x-\frac{π}{6}})$的图象,只需将函数y=cos3x的图象( )
| A. | 向右平移$\frac{2π}{9}$个单位 | B. | 向左平移$\frac{2π}{9}$个单位 | ||
| C. | 向右平移$\frac{2π}{3}$个单位 | D. | 向左平移$\frac{2π}{3}$个单位 |
13.下列函数中是奇函数的是( )
| A. | y=x+sinx | B. | y=|x|-cosx | C. | y=xsinx | D. | y=|x|cosx |
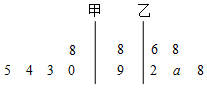 如图是甲、乙两位同学高二上学期历史成绩的茎叶图,有一个数字被污损,用a(3≤a≤8且a∈N)表示.
如图是甲、乙两位同学高二上学期历史成绩的茎叶图,有一个数字被污损,用a(3≤a≤8且a∈N)表示.